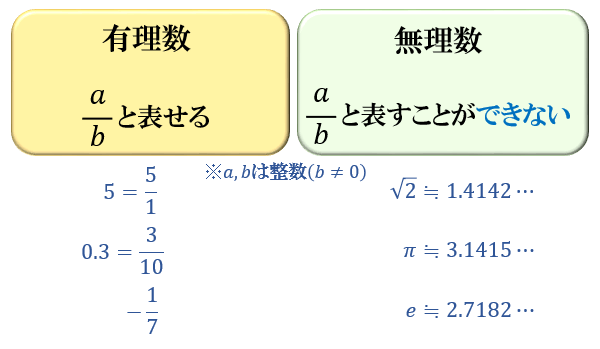
ルート2が無理数である証明 ここまでは「2つの整数 a , b を使って a b と表せる数」である有理数を見てきました。 その反対で「2つの整数 a , b を使って a b と表すことができない数」が、無理数です。 代表的な無理数としては、 2 の正の平方根 2 ≒ 1414 がただし,ルート2,ルート3,ルート5の近似値とその語呂合わせは非常に有名なので教養として覚えておくとよいでしょう。 平方数でない正の整数 n n n に対して n \sqrt{n} n は無理数(→ルート2が無理数であることの4通りの証明)なので小数は無限に続きます。 無理数とは有理数ではない数のことです。有理数は分数\( \displaystyle \frac{a}{b} (a,b \in \mathbb{Z} , b \neq 0) ~\) で表せる数のことなので、無理数は分数で表せない数と言うことができます。 教科書に載っている証明方法や、素因数2に注目した証明方法はこちら

背理法 を使いこなして証明を書こう ルート2が無理数であることの証明 についても解説 ますますmathが好きになる 魔法の数学ノート
ルートにが無理数であることの証明
ルートにが無理数であることの証明- 無理数になるんでないべか、と思う人もいるかもしれませんが 適当な有理数 a と無理数 b について (ab)(ab) = 2a となって、(2) の結果から ab と ab は無理数であることにより、無理数の和が有理数になりましたっ! こんにちは、ウチダです。 今日は数学Ⅰ「集合と命題」で習う 「背理法」 について、簡単に原理を説明した後、 「 $\sqrt{2}$ が無理数である」 ことの証明問題など、 よく出る問題 $3$ 選 を順に解説していきます。 また、記事の後半では、背理法と対偶証明法の原理に迫り、それらが本質




高校数学 背理法 無理数であることの証明 有理数と無理数の等式 A B K 0 受験の月
が無理数である ことの証明(高校教科書に多くある例) 証明) が無理数でない,つまり,有理数であると仮定すると, は既約分数で表すことができる すなわち,互いに素な(1以外に公約数を持たない)整背理法(ルート2、ルート3の証明) 問題 は無理数であることを証明せよ。 ただし, を自然数とするとき, が2の倍数ならば は2の倍数であることを用いてよい。 解答 が有理数であると仮定すると ( は互いに素な自然数) とおける。 両辺を二乗背理法被害者の会 新設 07月06日 脱背理法 と大学入試問題 脱背理法と大学入試問題 この頁のみ見る方のため、他の頁と重複することも書きます。 十数年前から脱背理法教育 (通常背理法で証明される定理を背理法を用いず証明する)を 東京理科大学数学
本稿では、 √2 2 が 無理数 であることの証明を紹介します。 √2 2 が 有理数 であると仮定すると、互いに素な整数 p,q p, q を用いて √2 = p q 2 = p q と表すことができます。 log 10 2が無理数であることの証明 log 10 2が有理数であると仮定する。 log 10 2>0より 自然数 n,mを用いて とおける。 整理すると 両辺m乗 すると2 m =10 n 右辺は5で割り切れるが左辺は5で割り切れない。 よって矛盾 背理法よりlog 10 2は無理数である。 円周率が無理数であることの証明 を行います。 この問題に取り組むにあたって、部分積分を何度も使用しますので、部分積分に慣れていない方はこちらを見て部分積分の計算に慣れましょう。 計算に慣れていないと泥沼にはまり込んでしまいます
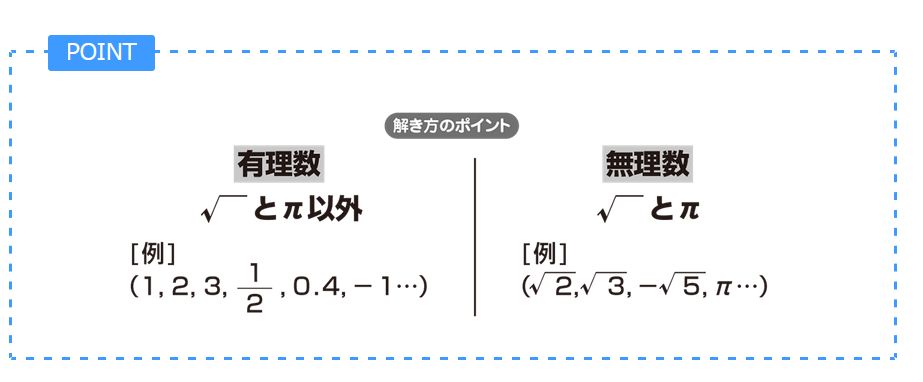
中3です。有理数と無理数の見分け方がいまいちわかりません。 なにかわかりやすい簡単な見分け方や、コツなどを教えていただきたいです。 / もし分数にして表現できる場合は有利数です。それ以外の数は無理数です。 平方根をとる(ルートに入れる)とき、ルート9=3E e が無理数であることの証明 タイプ: 難関大対策 α α レベル: ★★★★ e e が無理数であることの証明を,高校範囲と大学範囲でそれぞれ紹介します.大学範囲はたくさん情報がありますが,高校範囲は情報が少ないです. e e の定義に関しては √6 が無理数であることの証明の仕方。 互いに素のすべての自然数の組 m, n について、 ● m が 6 の倍数の場合、 m, n は互いに素だから、n は 6 の倍数でないので、n^2 は 6 の倍数でない。 一方、m は 6 の倍数だから、m/6 は自然数なので、 (m/6)^2 は自然数。



無理数はなぜ存在するのですか Quora



2が無理数であることを用いて 3 2が無理数であることを Yahoo 知恵袋
ルート2 は無理数である を証明するとき、背理法を使って矛盾を証明するとき ルート2 =b分のa(ただしabは互いに素の自然数とする) bを移行して二乗すると 2×bの二乗=aの二乗になる ここで矛盾が生じてルート2 は無理数であることが証明されたって聞いたんですがどうゆうことですか ルート2が無理数であることの4通りの証明 高校数学の美しい物語 で4つの証明が紹介されていた。 1番目はよくある偶数を使ったもの。 2番目を引用する。 √2 が 有理数 √2 = a b を満たす整数 a, b が存在する なので, a2 = 2b2 を満たす整数 a, b が存在し 背理法について説明するときには、「ルート2が無理数であることの証明」が使われることが多いです。 このサイトでも、 基本背理法 で使いました。 ただ、別に背理法を使わなくても、直接示すこともできます。 ここではその方法を紹介します




有理数とは 無理数とは 定義を明らかにして が無理数と証明する 数学ia Himokuri



有理数と分数 無理数の違い よくある誤解を越えて 趣味の大学数学
円周率πが無理数であることの証明 円周率 (円の周の長さと直径の比)が無理数である, つまり (整数)/ (整数) と分数の形で表せないことはよく知られています √2 2 や, log10 2 log 10 2 が無理数であることの証明は高校でもならいますが, 円周率 π = a, bがともに偶数となるので、これは互いに素であることに矛盾する。 したがって 2 は無理数である。 2 5 は無理数である。 2 5 は無理数ではない。すなわち有理数であると仮定し、有理数cを用いて 2 5 =c とする。 変形して 5 = c − 2 両辺を2乗して 5 = c 2円周率が無理数である事の証明が載ってるページ無かったっけ? 217 :132人目の素数さん: 2321 log(2)が無理数であることの証明とかってどうやってするんでしょ? マジレスキボンヌ。 218 :132人目の素数さん: 2326 >>217 log(2) = 1



1



無理数の発見の歴史
問題 n を平方数ではない自然数とする。 (平方数とはある自然数の2乗で表すことのできる数のことです。) このとき, n の平方根 n は無理数であることを証明してください。 難易度 素数と合成数 の練習無理数であることの証明 ルート2の証明 背理法 を使って、ルート2が 有理数 でないことを証明してみましょう。 まず、 ルート 2が有理数だとします。 すると、 ルート2は 自然数 の分子・分母で構成された 既約 分数 で表現できます。 (2)1/2=P/ Q 例題1からの流れで\( \sqrt{2} \)が無理数であることは使ってよいが\(\sqrt{6} \)が無理数であることはわからない場合、例題1と同様にして\(\sqrt{6} \)が無理数であることを示した後にやればいいのですが、 \(\sqrt{2} \)のみしか無理数であることがわかってなくても示す方法はあります。



ルート2が無理数であることを証明するために背理法を使いますが その時にルート Yahoo 知恵袋



Q Tbn And9gcrjivucysi8adty2sx1gwamoiji4a0zj0hl6iv2nwnkbw2wypri Usqp Cau
問 次のことを証明せよ (1) √2 は無理数である(2) √6 は無理数である解法の丸暗記に嫌気がさしたときに見る動画。解答の背後にある考え方を 無理数の例2 「平方根(ルート)」 中3数学でならった 「平方根」 も無理数だよ。ルートとよばれてるやつだ。 ルートがついているやつはたいてい無理数だね。 たとえば、良く登場してくる、 ルート2 は圧倒的に無理数だね。 なぜなら、 無理数の代表として挙げられる √2 2 。 この √2 2 が無理数であることの証明を2通り紹介します。




3が無理数であることを既知として 3 5が無理数であることを証明せ 数学 教えて Goo
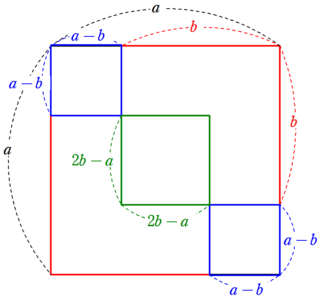



2が無理数であることの証明 面積の利用 Fukusukeの数学めも
ルート2が無理数であることの証明 Tooda Yuuto 17年10月23日 / 18年11月9日 有理数は英語で Rational Number 、無理数は英語で Irrational Number と言います。 無理数の代表として挙げられる\( このことを用いて、ルート7は無理数であることを証明せよ。 教えてください! 数学 √5√7は無理数であることを証明せよ、ただし√7は無理数であることは知られているものとする。 と言う問題で、√5√7を無理数でないと仮定して解いていたのですがまず無理数と証明するために有理数だと仮定しますよね? 有理数であると言うことは必ず分数で表せれます とすると循環小数も分数で表わせれるので有理数ですね そうすると分数にできないと言うことが証明でき√3は無理数だということが証明できます




高校数学 無理数であることの証明 背理法 練習編 映像授業のtry It トライイット



背理法とは 例題を証明しながら徹底的に解説します Studyplus スタディプラス
有理数全体が稠密集合なのだから無理数全体も稠密集合なはずです。 無理数が稠密であることの証明を3通り紹介します。 証明1 2 \sqrt {2} 2 は無理数( →ルート2が無理数であることの4通りの証明 )なので, 2 \sqrt {2} 2 2の3乗根が無理数であることの証明(背理法) $\sqrt3{2}$ が無理数であることを示してみましょう。基本的には、 $\sqrt{2}$ が無理数であることの証明と同じ流れです(参考:基本背理法)。 大きな方針としては、「もし有理数だったら矛盾することを示す」という背理法を使った証明です。が無理数であることの証明 (m≦17 or m<17, m≠平方数) デモクリトス BC 460 頃 BC 370 頃 「無理直線と立体」 テアイテトス BC 417 BC 369 m≠平方数 のときに が無理数であることの証明 ユークリッド原論の第 10 巻、第 13 巻の元々の著者 ?



阪大入試問題 円周率が無理数であることを証明する




九州大 背理法 超わかる 高校数学 A 演習 論理と集合 22 Youtube




背理法とは 無理数の問題例と証明を徹底解説 理系ラボ




無理 数 と は



三石 数学塾 ルート2が無理数であること



無理数を求める



背理法とは この例なら どんな馬鹿でも背理法が分かる 学生による 学生のための学問




2の平方根 Wikipedia



Pは無理数 の証明 怜悧玲瓏 高校数学を天空から俯瞰する




なぜ二乗して 3分の1が出てくるのか教えてください Clear




Pは無理数 の証明 怜悧玲瓏 高校数学を天空から俯瞰する
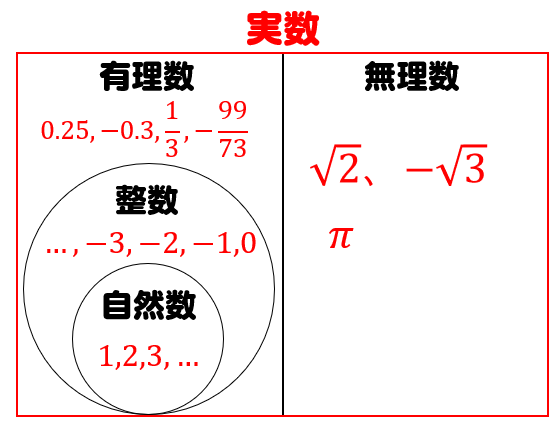



有理数 無理数とは 違いを簡単に解説 中学生が覚えるべき無理数は2種類だけ 数学fun




Sin1 Cos1 は無理数か 世界変動展望



ルート2が無理数であることを背理法を使って証明せよ Yahoo 知恵袋




数学 B 指数と累乗根の性質に関する問題 尾道市立大 京都教育大 横浜市立大 ページ 2 大学入試数学の考え方と解法



3が無理数であることを用いて 1 3が無理数であることを証明せよ あとこ Yahoo 知恵袋




中学数学 平方根 のコツ 有理数と無理数 循環小数と分数



ルート2が無理数であることの証明 数式で独楽する



有理数と無理数の違い ルート2が無理数であることの証明 アタリマエ




12年京大入試理系数学第4問 ほのぼの数学がんばろう




数学 背理法による証明の解答例まとめ 数スタ



5が無理数であることを 背理法を用いて証明せよ 5が無理数 Yahoo 知恵袋




命題 背理法を用いたルート2が無理数であることの証明 高校数学マスマスター 学校や塾では教えてくれない 元塾講師の思考回路の公開




2が無理数であることの図形的な証明 理系のための備忘録




無限降下法とは フェルマーの最終定理などの応用例3選を解説 遊ぶ数学




無理 数 と は 無理数 むりすう とは Docstest Mcna Net




ルート2が無理数であることの証明 数式で独楽する




数a 2が無理数であることを証明せよ 背理法 Youtube




高校数学 背理法による証明の書き方 手順 具体例を使ってわかりやすく解説 楽スタ




ルート2が無理数であることの4通りの証明 高校数学の美しい物語




6が無理数であることを用いて 次の命題を証明せよ Clear
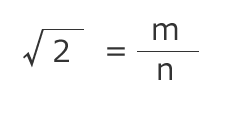



2が無理数である証明 実数 有理数 無理数 優技録




有理数と無理数の違い ルート2が無理数であることの証明 アタリマエ



11 有理数 無理数の問題 京極一樹の数学塾




無理数 Wikipedia




高校数学 背理法 無理数であることの証明 有理数と無理数の等式 A B K 0 受験の月
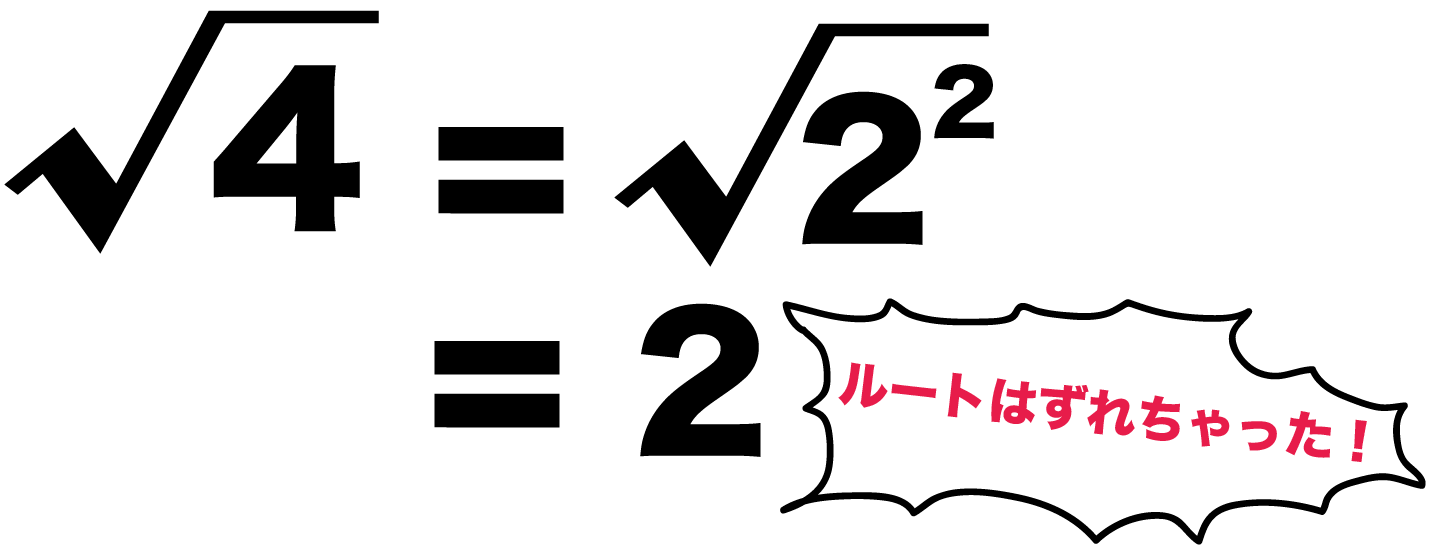



中3数学 有理数と無理数とはなんだろう Qikeru 学びを楽しくわかりやすく




ルート2が無理数であることの4通りの証明 高校数学の美しい物語




無限降下法 05 首都大学東京 後 イズミの数学




2が無理数であることの2つの証明 Youtube




高校数学 数 33 命題 続 背理法編 Youtube




中3数学 有理数と無理数とはなんだろう Qikeru 学びを楽しくわかりやすく




A B N A B Nの重要な性質の証明と入試問題への応用を解説 東大医学部生の相談室




高校数学 無理数であることの証明 背理法 練習編 映像授業のtry It トライイット




ルート3が無理数であることを証明せよ 世界変動展望




もたこ博士の算数工房 算数から数学まで




ルート2が無理数であることの4通りの証明 高校数学の美しい物語



三石 数学塾 ルート2が無理数であること その2



Q Tbn And9gcsoivj3hkpes2bz0ua1tr2vkogwtievhvapjv3bvj90lec7tci7 Usqp Cau
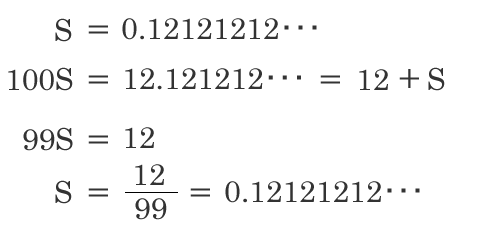



2が無理数である証明 実数 有理数 無理数 優技録




有理数と無理数の違い ルート2が無理数であることの証明 アタリマエ




背理法を利用してルート3が無理数であることを証明する問題で1以外に正の公約数をもたな Clear




背理法とは ルート2が無理数である証明問題などの具体例をわかりやすく解説 排中律 遊ぶ数学




結城浩 そういえば 数学ガール フェルマーの最終定理 には背理法の章があって どういう問題にしていたかというと 無理数で あることの証明 ではなく 有理数ではないことの証明 にしていました



無理数とお友達になろう 第384回科学勉強会




背理法 を使いこなして証明を書こう ルート2が無理数であることの証明 についても解説 ますますmathが好きになる 魔法の数学ノート




発展 無理数の無理数乗は無理数か なかけんの数学ノート



2016年 東大理系数学 第5問 具体的に調べる スケール 整数の存在証明 ガウス 背理法 オンライン受講 東大に 完全 特化 東大合格 敬天塾




中学数学3年 平方根とその近似値 大小 有理数と無理数 受験の月



Q Tbn And9gcsk Pb4fz2a Hve1dkvnyto1a4rswurwiisfdfuogu0o6rlolcb Usqp Cau



6が無理数であることの証明の仕方教えてください ただし Yahoo 知恵袋




有理数と分数 無理数の違い よくある誤解を越えて 趣味の大学数学




ルート5は無理数であることを証明せよ っていう問題なんですが これであってますか Clear




演習問題 ルート2が無理数であることの証明 背理法 Youtube



Grb1f Htm




無理数の無理数乗 有理数となる場合 年 横浜市立大 1986年 阪大 数学日和




有理数と無理数の違い ルート2が無理数であることの証明 アタリマエ
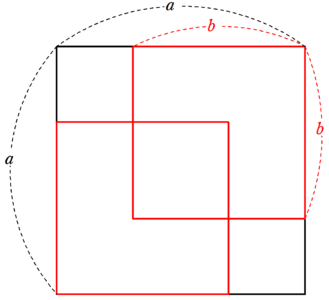



2が無理数であることの証明 面積の利用 Fukusukeの数学めも




無理数とは 知恵袋




無理数とお友達になろう 第384回科学勉強会




もたこ博士の算数工房 算数から数学まで




3分で分かる 有理数と無理数の違いと見分け方 練習問題付き 合格サプリ



福田のわかった数学 高校1年生033 背理法 1 Okedou




無理数とお友達になろう 第384回科学勉強会




無理数の無理数乗 有理数となる場合 年 横浜市立大 1986年 阪大 数学日和



三石 数学塾 ルート2が無理数であること




ルート2が無理数であることの証明 数式で独楽する




背理法とは ルート2が無理数である証明問題などの具体例をわかりやすく解説 排中律 遊ぶ数学




例題58の解説でr 7を二乗する時に R 7 で計算するのはなぜですか 教えて Clear




数学の卵 Euler L Twitter



三石 数学塾 ルート2が無理数であること その2




数学基礎1 3 有理数と無理数




5が無理数であるユニークな証明 黄金比 Youtube



背理法とは 例題を証明しながら徹底的に解説します Studyplus スタディプラス



ルート2が無理数であることを背理法を使って証明せよ Yahoo 知恵袋




2が無理数であることを背理法を使わずに証明できますか Quora




ルート2が無理数であることの証明 数式で独楽する



数学の問題です ルート6が無理数である ことを用いて ルート3 Yahoo 知恵袋




2が無理数であることを証明 2を有理数と仮定した時なぜ1以外の公約 数学 教えて Goo




有理数とは 無理数とは 定義を明らかにして が無理数と証明する 数学ia Himokuri



11 有理数 無理数の問題 京極一樹の数学塾




背理法とは 例を使って慶應生がわかりやすく解説してみた 高校生向け受験応援メディア 受験のミカタ



0 件のコメント:
コメントを投稿