一次方程式の文章問題 個数と代金についての練習問題です。 解説記事はこちら gt;一次方程式の利用問題解き方まとめ スポンサーリンク 目次1 方程式練習問題一次方程式の文章問題~個数と代金~2 練習問題の解答& 単元:1次方程式 利用問題 中学生数学特訓プラン 基礎力養成特訓プラン 推奨学年中学1年~中学3年生内容計算の基礎養成演習時間割50分授業×週1回授業回数月間4回授業料中学1年生:8,300円中学2一次方程式、式の展開・因数分解 音声付き電気技術解説講座 公益社団法人 日本電気技術者協会 一次方程式は、一つまたは複数の変数の関係を表す方程式で、いずれの項も変数の一次式の和または差で表される。 定数が一定の線形電気回路の電圧と
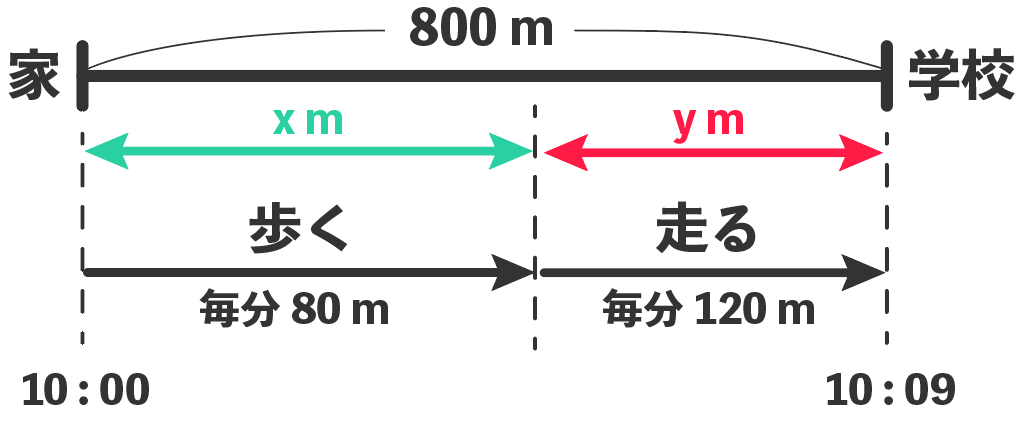
連立方程式の利用 速さ 道のり 時間の文章問題の解き方 Qikeru 学びを楽しくわかりやすく
一次方程式の利用 問題 難問
一次方程式の利用 問題 難問- ここでは、一次方程式を利用して問題を解く方法を見ていきます。何かを買う場面を扱います。 一次方程式を利用して問題を解く 基本一次方程式の解き方では、次のような一次方程式を解く方法を見ました。 1x140=5方程式をつくることができる。(技能) 一元一次方程式を解くことができる。(技能) 3 ①´=②´より方程式を解く ・生徒の人数を求めた後,あめの個数についても求めさせる。 4 この解は問題にあっている。 よって, 生徒は8人




中学2年生 数学 連立方程式の活用 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
一次方程式のグラフ 連立方程式の解と一次関数のグラフの交点 一次関数の利用(水温、ばね、道のり・速さ・時間、動点) *「ページ表示」を「見開き」でご覧いただきますと問題とその答えが見やすく なります *このテキストは家庭学習の補助教材と数学22章連立二元一次方程式「連立方程式の利用」<準備問題①> 組 番 名前 1次の問いに答えなさい(ただし,もっとも簡単な式に表しなさい。) (1)長さ2mのひもの端から,長さ25cmのひもをχ本切り取ると,残りのひもの長さはy㎝で した。 中学数学の基本「一次方程式」。 方程式の「利用」や「応用」というかたちで、文章問題が出題される単元でもあります。 別の記事でご紹介した通り、文章問題は主に8種類。 初めて訪問してくれた皆さんのために
一次方程式の文章題ー速さ 速さに関する1次方程式の文章題の練習問題です。 *問題を解く前に小学校で習った速さの公式、時間の単位などを確認しましょう。 方程式の文章題の解き方は 何をxとおくか考えてみる。 数学13章一元一次方程式「一次方程式の利用」<準備問題①> 組 番 名前 1次の問いに答えなさい。 (1)ある数に17をたしたら30になります。ある数を求めなさい。 4 1 (2) mのテープがあります mずつ切ると,何本のテープができるか求めなさい。<前:L25 一次関数の利一次方程式 大小関係を表す式 132 1 次の に当てはまる言葉を書きなさい。 不等号を使って数量の関係を表した式を といいます。 { 2 次の数量の関係を不等式で表しなさい。 (1)xの5倍は30より大きい
一次方程式の利用 小学校の教科用図書などから、一元一次方程式を用いて解 数学的活 ・具体的な問題を一次方程式 くことのできる問題を示し、小学校での解決の仕方と比較 動 を利用して解くときの考え し、方程式を用いて解くことのよさを味わわせる。 ・一次方程式の解き方 ・一次方程式の練習問題 ・一次方程式の文章問題 ・一次方程式の大切さ を見ていました。 中学1年生の内容だからといって侮ってはいけません。計算練習をしてしっかりと一次方程式を解くコツを掴んでください。あなたが一次方程Z一次方程式 z等式の性質 z方程式の解き方 z方程式の利用(個数と代金、道のり・速さ・時間、年齢、整数) z比例式(移行措置による追加) z方程式の利用(割合、食塩水の濃度) *「ページ表示」を「見開き」でご覧いただきますと、問題とその




連立方程式の利用の問題の解き方 年齢の問題 1 現役塾講師のわかりやすい中学数学の解き方




一次方程式の利用 道のり 速さ 時間の文章題の解き方は 中学数学 理科の学習まとめサイト
Pocket 今回は、中1で学習する『一次方程式の文章問題』の中から 年齢を求める問題について解説していきます。 Aくんは13歳、Aくんのお父さんは43歳です。 お父さんの年齢がAくんの年齢の2倍になるのは何年後か。 また、そのときのAくん、お父さんの方程式と解の意味を知り, 等式の性質を用いた一次方程式の解法を理解し, 一次方程式 を解くことができる。 一次方程式を具体的な問題の解決に利用することができる。 数学への 関心・意欲・態度 数学的な見方や考え方 数学的な技能 数量や図形など ID非公開 さん 21/8/27 2355 0 0 回答 中学2年生 数学 一次方程式の問題です。 ⑵の問題の解き方が分からないので教えていただけると嬉しいです。 解答 ⑴ 5/4 × a 5 ⑵ 2 中学2年生 数学 一次方程式の問題です。 ⑵の問題の解き方が分からないので




方程式の利用の問題の解き方 代金の問題 1 現役塾講師のわかりやすい中学数学の解き方




中1 数学 中1 37 方程式の利用 追いつく編 Youtube
方程式の問題を解く。 方程式の利用の問題をとく手順①~④を確 認する。 本時のめあてを確認する。 課題意識をもたせる。 ・問題を見て,意味を考える。 6個買ったら130円あまりました。ハンバ ・繰り返し読ませる。数学13章一元一次方程式「一次方程式の利用」<準備問題①> 組 番 名前 1次の問いに答えなさい。 (1)ある数に17をたしたら30になります。ある数を求めなさい。 4 1 (2) mのテープがあります mずつ切ると,何本のテープができるか求めなさい。このように、方程式の解が問題の答えでないこともある。 一次方程式 方程式のうち、一次式で方程式があらわされる式のことを一次方程式(いちじ ほうていしき)といいます。 ax b = 0 (aは0以外の数) や ax b = c (aは0以外の数)



1
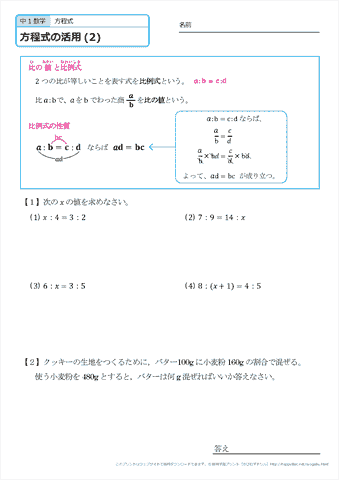



中学1年生 数学 方程式の活用 比例式 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
(4) 一次方程式を解く手順を まとめる。 質まで立ち返って指導する。 2 方程式の利用 <1>方程式を利用して,い ろいろな問題を解く。⑤ (1) 方程式をつくる手順を考 える。 る。 線分図を用いて数量の間の関係 をつかませ, の代わりにxを使方程式の導入 等式の変形 中学数学移項と様々な1次方程式 中学数学1次方程式の解法・決定版 中学数学方程式の利用・文章題での解答の書き方 中学数学方程式の利用・代金と個数 中学数学方程式の利用・数に関する問題 中学数学連立方程式 連立方程式の利用<文章問題の基本> ⇒ 解説・解答 連立方程式の利用<応用1> ⇒ 解答・解説 連立方程式の利用<応用2> ⇒ 解答・解説 1次関数 一次関数を求める問題 ⇒ 解答・解説 一次関数の問題(1) ⇒ 解答・解説




中学2年生 数学 連立方程式の活用 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




方程式の利用 一次方程式の文章題の4つの解き方 Qikeru 学びを楽しくわかりやすく
一次方程式の解の求め方 "一次方程式"は中学校1年生の数学で習いますが、今後習う"連立方程式"や"二次方程式"などを解くための基盤となる重要な単元です。 ただ 等式の性質を利用して「 x = x = 」の形に変形します。 丁寧に変形していくと以下方程式 文章問題 速さ・時間・道のり(距離)の計算 //googl/KzS8NA中1数学の一次方程式の利用。追い越す、出会う 速さの文章問題をわかりやすく方程式利用代金の文章問題を解く方法について解説! 方程式利用年齢の求め方は?文章問題を解説! 比例式の解き方まとめ!かっこがついている計算方法は? 比例式の文章問題を解説!




一次関数の利用 追いつく速さの文章問題を解説 数スタ




中学数学 1次方程式 文章題の解き方 代金 個数
3章 1次方程式 2.1次方程式の応用 1方程式を利用した文章題の解法の手順 ①問題をよく読み、わからない数量を\(x\) とおく。 ②等しい数量の関係をみつけて、方程式を作る。 ③方程式を解く。 ④方程式の解が問題に適しているか確かめる。 利用問題(文章題)の解き方を簡単に解説! 21年2月19日 この記事では「一次方程式」の解き方についてできるだけ簡単に解説していきます。 分数を含む一次方程式や、一次方程式を利用する文章題の解き方もわかりやすく解説していきますので、この4 1次方程式の利用 ④方程式を利用して、具 体的な事象の中の問題 を解決しようとする。 ⑤具体的な事象の中の数 量の関係を捉え、方程 式をつくることができ る。 ⑤代表的な問題につい て、題意にあった方程 式をつくることができ る。 ⑥解を吟味する




方程式 速さの問題 追いつくのは何分後 解き方を解説 中学数学 理科の学習まとめサイト



連立方程式の文章題 代金 チーム エン
等式の性質 方程式の解き方 かっこのある方程式 係数が小数の方程式 係数が分数の方程式 比例式 方程式と解 文章題 連続する整数 文章題 2けたの自然数 分配に関する問題 文章題 買い物 文章題 買い物2 過不足 平均 年齢 文章題(速さ)追いつく 文章題(速さ ここでは、一次方程式を利用して解く問題を見ていきます。平均に関する問題を見ていきます。 平均に関する問題その1 例題1 あるクラスには、男女合わせて40人の生徒がいます。このクラスで数学のテストを行ったところ、男子の平均第3章 方程式 << L 不等式 の問題に戻る L21 一次方程式の活用(1) の解答表示 >> 練習問題1 ある中学校の生徒数は250人で男子は女子より14人多いそうです。 これについて以下の問いに答えなさい。 1 女子の人数を x として、方程式を作り




連立方程式の利用 文章題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




中1 1次方程式の利用 中学生 数学のノート Clear
中学校1年 の数学で習う「一次方程式」の文章問題集です。 問題の数値はランダムで生成することができ、答えの表示・非表示も切り替えられます。印刷してご活用ください。 ちなみに一次方程式の解き方について詳しい解説はこちらに説明しています。問題を方程式を 利用して解く。 方程式を利用す ることに関心を 持ち,問題を解 決しようとして いる。〔観察・ノ ート〕 問題の中の数 量の関係をと らえ,方程式を つくることが できる。〔観 察・ノート〕 10 ・代金の問題を方 程式を利用し て解く方程式をつくることができる。(技能) 一元一次方程式を解くことができる。(技能) 3 ①´=②´より方程式を解く ・生徒の人数を求めた後,あめの個数についても求めさせる。 4 この解は問題にあっている。 よって, 生徒は8人




2次方程式の応用問題の解き方 文章問題 数学fun
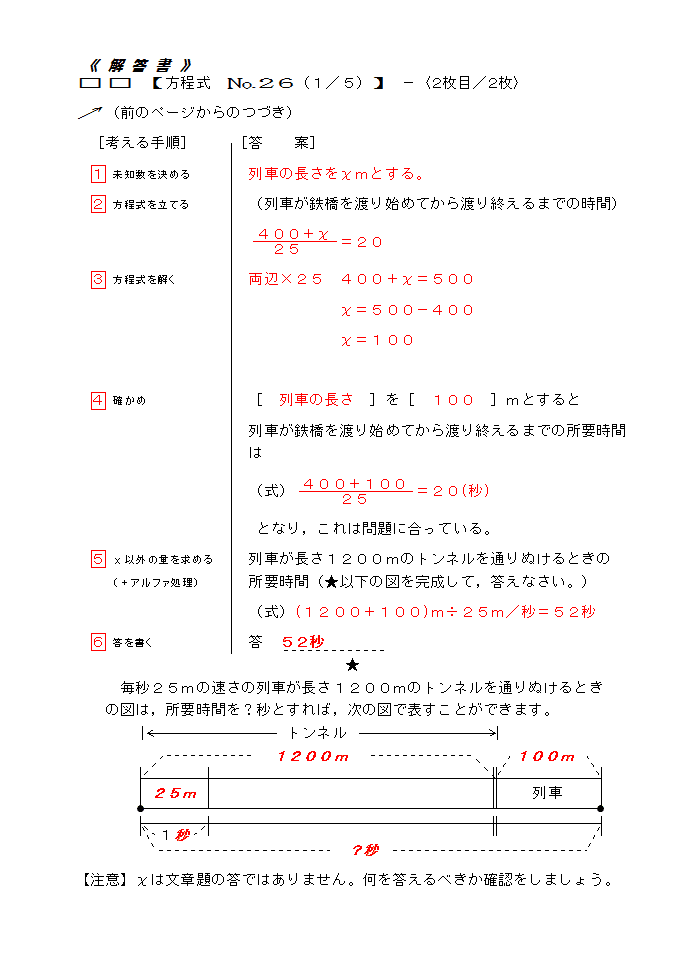



中1数学 方程式 26 1 中学数学高校数学個別指導in山形市 数専ゼミ



無料 中1数学 基本問題 問題プリント 方程式4 方程式の利用1 125




1次方程式 食塩水の問題の解き方 中学数学 定期テスト対策サイト




二次方程式の利用の問題の解き方 図形 5 現役塾講師のわかりやすい中学数学の解き方
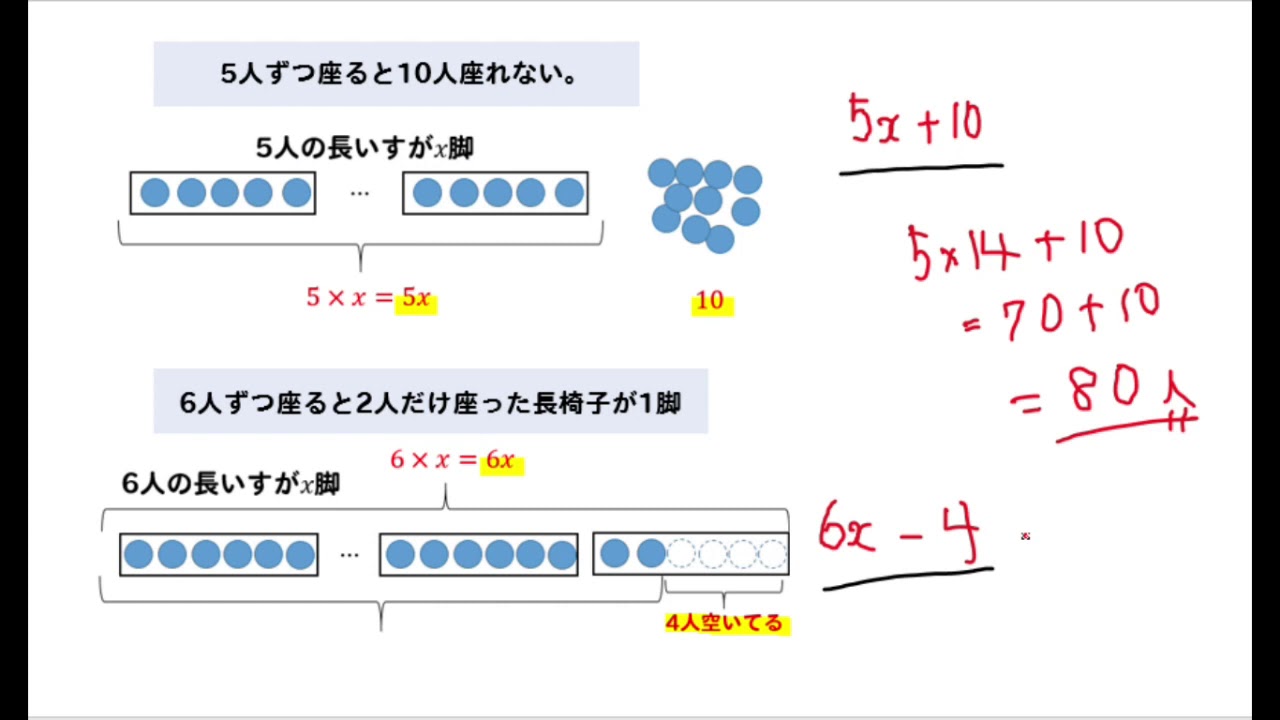



一次方程式の利用問題 解き方まとめ 方程式の解き方まとめサイト




連立方程式の利用 速さ 道のり 時間の文章問題の解き方 Qikeru 学びを楽しくわかりやすく




中学2年生 数学 連立方程式の解き方 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中学3年生 数学 2次方程式の活用 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中学数学1年 1次方程式の利用 速さ 時間 道のり 受験の月



1




中学数学 1次方程式 文章題の解き方 代金 個数



中1 一次方程式の文章題 中学数学の方程式 中間 期末テスト 高校入試対策



二次方程式の利用 文章問題の解き方がわかる4つのステップ Qikeru 学びを楽しくわかりやすく



2




中学数学 1次方程式 文章題の解き方 分配 年齢 貯金




中学2年生 数学 連立方程式の活用 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中学1年 数学 定期テスト練習問題 1次方程式の利用 赤城 ᐡᐤᐡ



1次方程式の利用の過不足についての問題ですが なぜx 2になるの Yahoo 知恵袋




誰でもわかる数学 中学1年 一次方程式の応用問題 Youtube




中学数学 1次方程式 文章題の解き方 代金 個数




中学1年生 数学 無料問題集 一次方程式 おかわりドリル



1次方程式の利用 買い物問題 デジタル教科書 電子教科書




基本 一次方程式の利用 速さ なかけんの数学ノート




連立方程式の利用の問題の解き方 平均の問題 1 現役塾講師のわかりやすい中学数学の解き方



無料 中1数学 基本問題 問題プリント 方程式5 方程式の利用2 126




一次方程式の文章題1 数 代金 過不足の問題 無料で使える中学学習プリント



無料 中1数学 基本問題 解答プリント 方程式5 方程式の利用2 126




中1 数学 中1 33 方程式の利用 お金編 Youtube




中学1年生 数学 無料問題集 一次方程式 おかわりドリル




一次関数の応用問題 動く点p チーム エン




二次方程式の利用の問題の解き方 整数 3 現役塾講師のわかりやすい中学数学の解き方




一次方程式の利用 文章問題 ポイントは3つだけ 苦手な数学を簡単に




方程式の利用の問題の解き方 過不足の問題 1 現役塾講師のわかりやすい中学数学の解き方




中学1年 数学 東京書籍 教科書 3章2節 1次方程式の利用 期末テスト用 赤城 ᐡᐤᐡ




中学1年の1次方程式の問題です Clear




中学数学1年 1次方程式の利用 年齢 受験の月




食塩水の濃度に関する連立2元1次方程式の応用問題 中学校2年生の数学より 身勝手な主張




一次方程式の利用問題 解き方まとめ 方程式の解き方まとめサイト
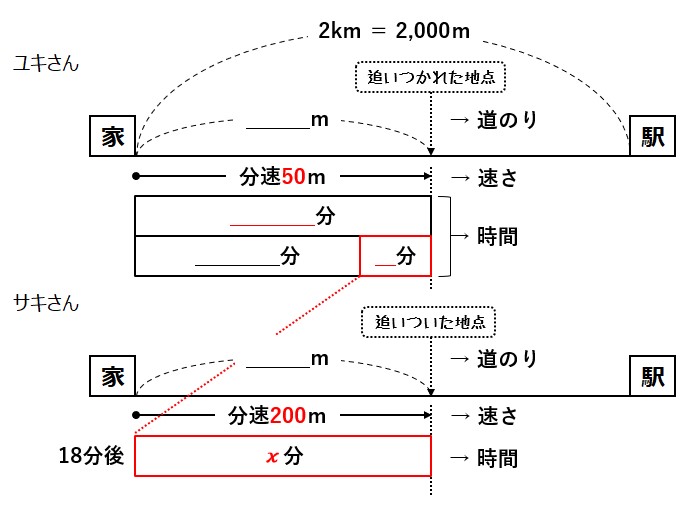



わかる 中学数学 一次方程式の利用 文章題 道のり 速さ 時間の問題 を丁寧解説




基本 一次方程式の利用 ものを配る なかけんの数学ノート




中学数学 1次方程式 文章題の解き方 速さ 時間 道のり




一次方程式の利用 文章問題 苦手な数学を簡単に




中学数学 1次方程式 文章題の解き方 代金 個数




詳しく 中学数学 一次方程式の利用 文章題 割合 濃度の問題 を解説




方程式利用 何分後に追いつくか 速さの文章問題を徹底解説 数スタ




中学数学1年 1次方程式の利用 食塩水の濃度 受験の月




方程式の利用 一次方程式の文章題の4つの解き方 Qikeru 学びを楽しくわかりやすく




二元一次方程式の文章題のやり方とこの写真の問題と 解き方を教えて欲しいです Clear




中学生 1次方程式の利用のノート一覧 Clear




中学2年生 数学 連立方程式の活用 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中学1年生 数学 方程式の活用 比例式 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
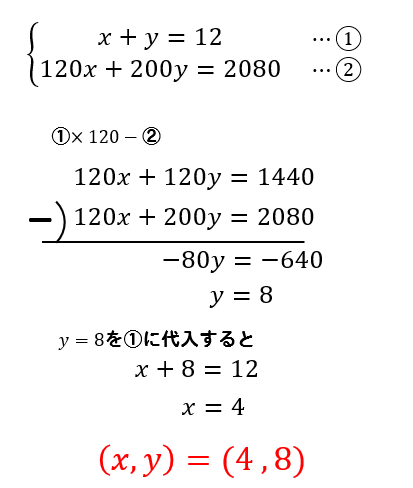



連立方程式の利用 文章問題 解き方まとめ 方程式の解き方まとめサイト




中学数学 1次方程式 文章題の解き方 代金 個数




数学 中2 連立方程式の利用 お金編 Youtube




一次方程式の文章問題がすごく苦手です Clear




中学数学 1次方程式 文章題の解き方 代金 個数




一次方程式の解の求め方 数学fun




比例式の文章問題 利用 の解き方を解説 数スタ



無料 中1数学 基本問題 解答プリント 方程式4 方程式の利用1 125




方程式の利用 一次方程式の文章題の4つの解き方 Qikeru 学びを楽しくわかりやすく




中学1年生 数学 方程式の活用 比例式 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中1 数学 1次方程式の利用 中学生 数学のノート Clear
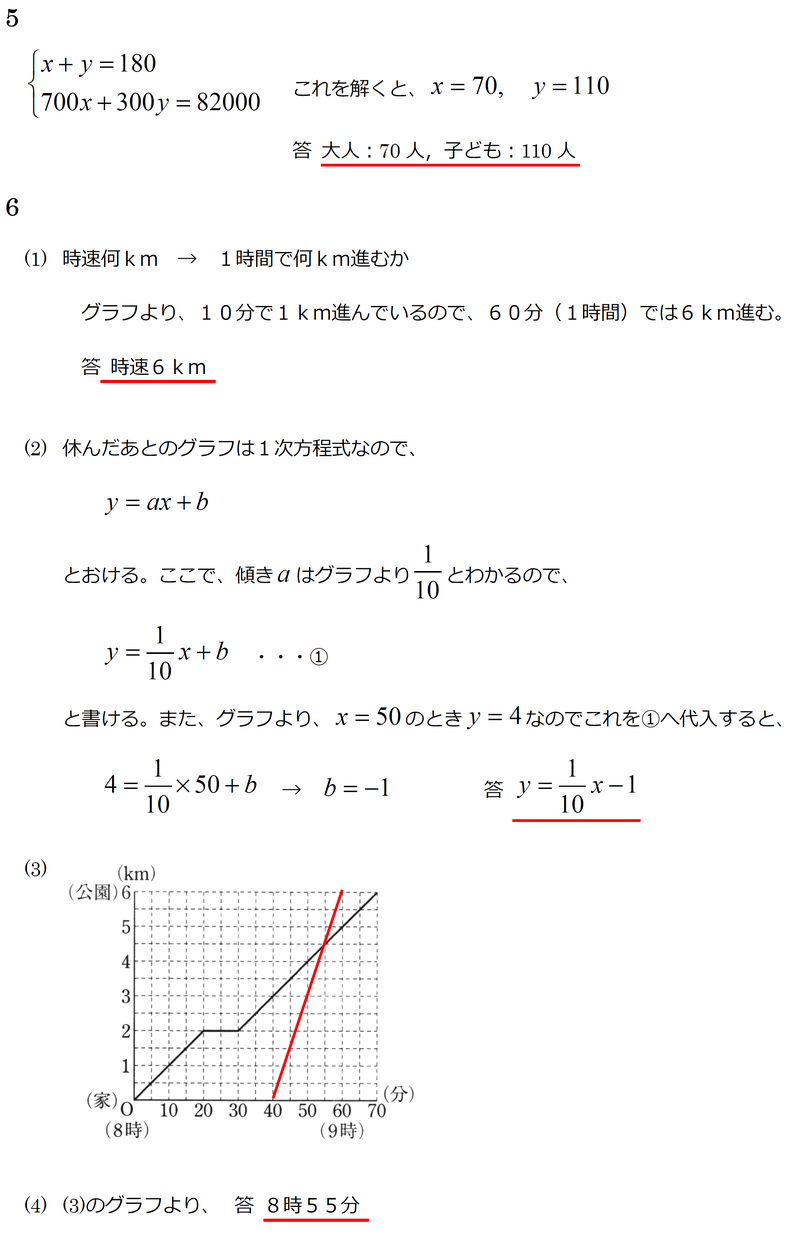



中学 数学 実力テスト 過去問 連立方程式 1次関数の利用 問題と解答 赤城 ᐡᐤᐡ




中1 数学 中1 38 方程式の利用 2つの速さ編 Youtube




方程式の利用 一次方程式の文章題の4つの解き方 Qikeru 学びを楽しくわかりやすく




1次方程式の利用 2 整数 過不足 年齢 割合の問題 Shun Ei Note




一次方程式の文章題1 数 代金 過不足の問題 無料で使える中学学習プリント




中1数学 方程式 15 2 中学数学高校数学個別指導in山形市 数専ゼミ




一次方程式とは 利用問題 文章題 の解き方を簡単に解説 受験辞典




連立方程式の文章題1 無料で使える中学学習プリント




方程式の利用 速さの問題 表を使った解き方 苦手な数学を簡単に
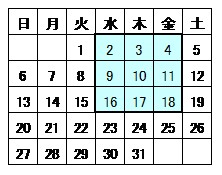



Math 1次方程式の利用 カレンダーの問題 働きアリ




一次方程式の文章問題の解き方 数学fun




中学数学1年 1次方程式の利用 個数と代金 受験の月



2次方程式の利用 図形 清水塾




数学 中2 23 連立方程式の利用 割合の基本編 Youtube




中学数学1年 1次方程式の利用 分配と過不足 受験の月
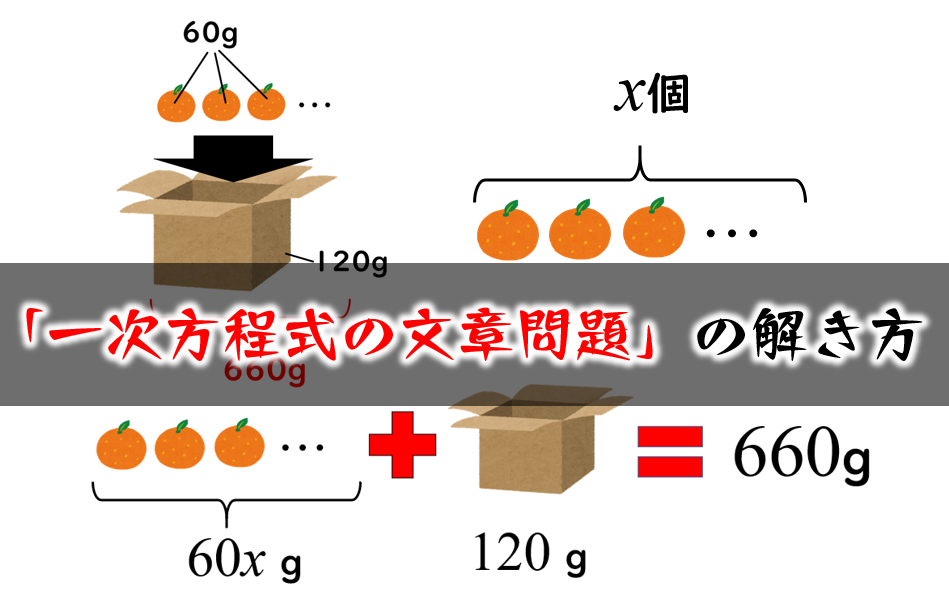



一次方程式の文章問題の解き方 数学fun




方程式 年齢の求め方は 文章問題を解説 数スタ



3
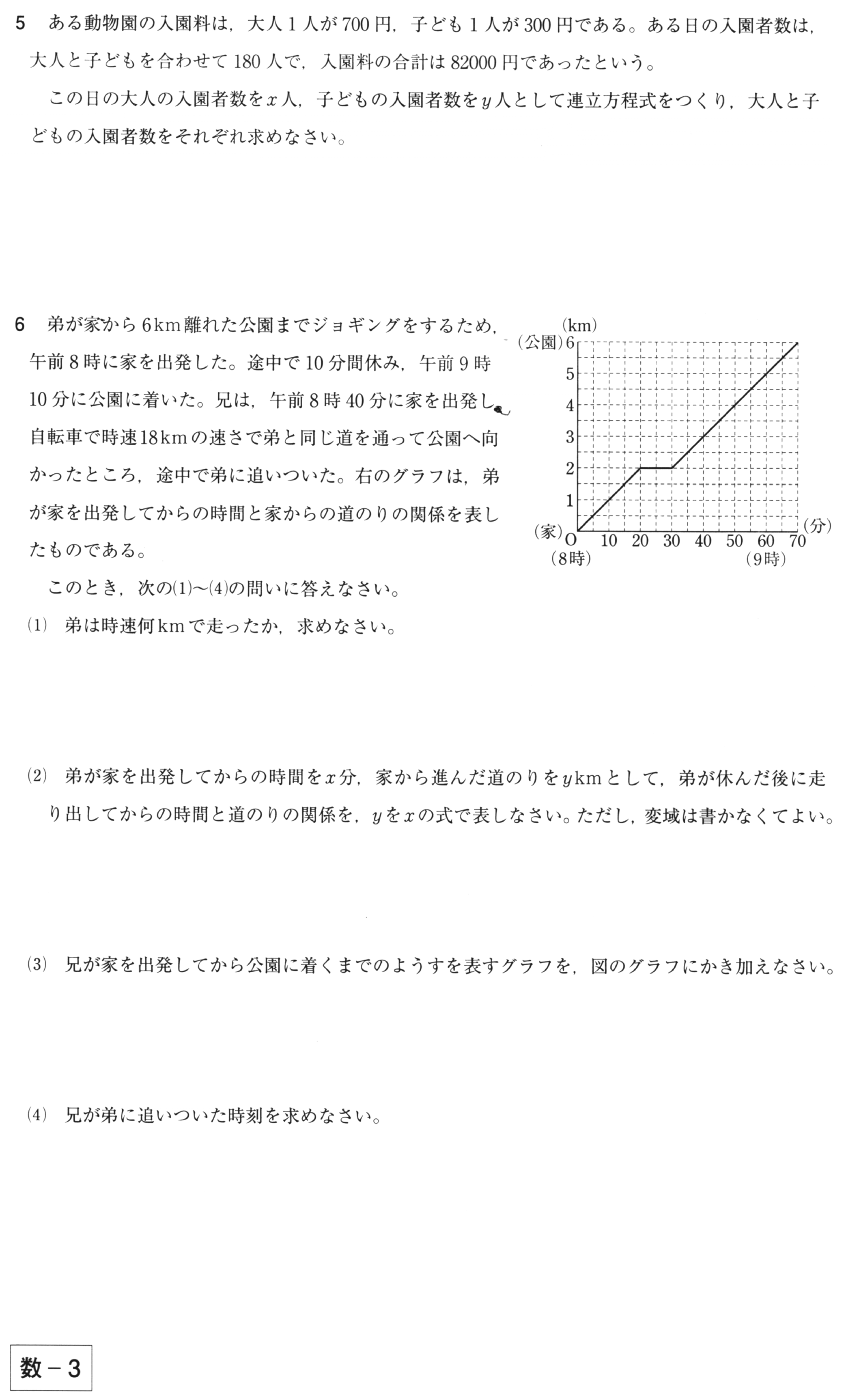



中学 数学 実力テスト 過去問 連立方程式 1次関数の利用 問題と解答 赤城 ᐡᐤᐡ




方程式の利用の問題の解き方 過不足の問題 2 現役塾講師のわかりやすい中学数学の解き方




國一 Junior High数学的 中1数学 1次方程式の文章題を解く流れ 筆記 Clear
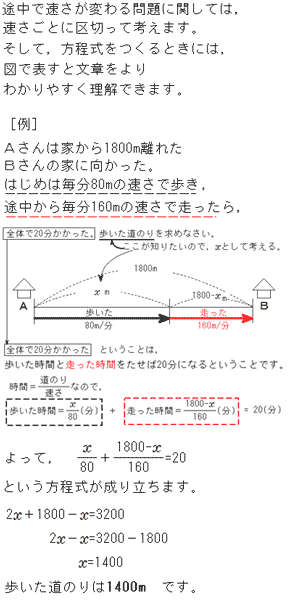



方程式 途中で速さが変わる問題の解き方 中学生からの勉強質問 数学 進研ゼミ中学講座




一次方程式の文章題1 数 代金 過不足の問題 無料で使える中学学習プリント



2



3




中1 数学 一次方程式の利用 3 道のり 速さの問題 Youtube




中1数学 方程式の文章題 速さ 例題編 映像授業のtry It トライイット



0 件のコメント:
コメントを投稿