角柱・円柱の表面積の求め方:中学数学の柱体の公式と展開図の計算 中学数学では空間図形を学びます。 平面ではなく、立体的な図形の面積や体積を理解するのです。 そうした分野の一つが柱体の表面積です。 柱体(角柱・円柱)の表面積はどのようにして計算すればいいのでしょうか。 柱体の表面積を計算するにしても、形によって表面積の計算方法は異なりや円柱に関心をも ち,その体積を調べ ようとする。 ・角柱や円柱の体積の 求め方について,直 方体の体積の求め方 から類推し,図や式 を用いて考え,表現 することができる。 ・角柱や円柱の体積を, 公式を用いて求める ことができる。 ・角柱や円柱19/2/14 高さの分からない円すい展開図! どうやって立体の体積を求めるの? 立体図形 立体図形 次の展開図から出来る円すいの体積を求めなさい 知りたがり 円すいの体積は、底面積 高さ ÷ 3
動画で学習 2 角柱と円柱の展開図 算数
円柱の展開図 体積
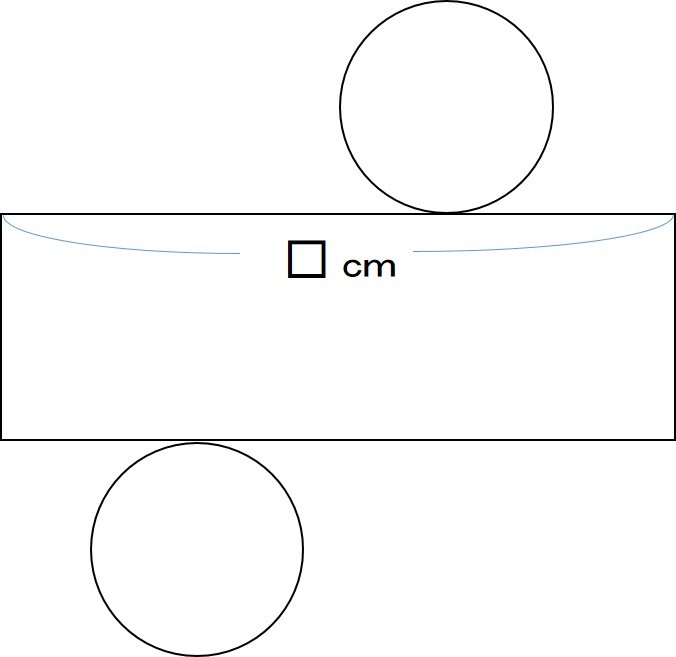
円柱の展開図 体積-真ん中の四角柱(直方体)の体積 \(8×8×15=960(cm^3)\) 右の円柱の体積 \(4×4× \pi ×15=240\pi(cm^3)\) 柱体の表面積 \(柱体の表面積=底面積×2側面積\) 下の円柱の表面積を求めてみましょう。 表面積を求めるときは、立体の展開図を考えるとよいでしょう。その正方形の対角線の長さはどれも同じ長さになるよ。 (2) 式 10 ×10 ×π×15 円柱の体積 1500π cm3 ポイント 円柱の体積は,次のように求めることができるよ。 (円柱の体積)=(円柱の底面積)×(円柱の高さ) 円柱の底面積は, (円柱の底面積)=(円の面積) 円の面積は, (円の面積)=(円の半径)×(円の半径)×(円周率) =10 ×10 ×π =100π だから, (円柱の体積)=100π×15




立方体や直方体の体積の求め方を習ったら 少し応用的な問題にも取り組みましょう 展開図を見て 体積を求める問題や いくつかの立方体や直方体の面積を足したり引いたりして解く問題です 学習ノート 小学校 算数 学習
47 7 立体の体積と表面積 133 次の図の直方体の体積と表面積を求めよ。 ⑴ ⑵ ⑶ 137 次の図の立体の体積と表面積を求めよ。 ⑴ ⑵ 135 次の図の円柱の体積と表面積を求めよ。 ⑴ ⑵ ⑶ 134 右 の図は ,円柱とその展開図である。 次の問いに答えよ。2 次の展開図を組み立てて、できあがる立体の体積を求めましょう。 ① 式 長方形の横の長さは、円周と同じ長さなの円柱の体積 π×3 2 ×4=36π (cm 3)からくぼみになっている円錐の体積 π×3 2 ×4÷3=12π (cm 3)を引くと V=24π (cm 3) 8 AB=3cm,BC=4cm,CA=5cmの直角三角形を,図のようにBCから3cm離れた直線DEの周りに1回転させとき, ABCが通ったあとにできる立体の体積は (cm 3 )
愛知県半田市教育委員会ictサポートページ デジタルコンテンツリンク 10年度「豊かな学びのためのcioを中心としたictサポート体制の在り方」研究発表のコンテンツを公開しております。Grapes3D利用して,実モデルではなく,図を次のように表した。 前回のレポートで,円柱の45°切断という,いわゆる非回転体の求積問題について,次のページのような問題を考えたが,その立体の"全体図"を考えたようなものと想像していただければと思う。 本レポートでは,計算の便宜上,半径1の円の底面をもつ,高さ2の円柱を切断することにする。 (1) 体積になコーンを考える。(図では、1個しかないが、これが球面 上密集しているような図を想像して下さい... f(^_^) ) このコーンの高さは、r に等しいとしてよい。 このとき、球の表面積 S と体積 V には
幾何 数学 立体 円錐 立方体 直方体 円柱 角錐 角錐 球面 曲面 体積 円柱展開図 新しい教材 2つの円の交点を通る円(グラフ) 数学デッサンワークショップ用⑨角柱と円柱の体積 角柱、円柱の体積の求め方と公 空間図形 ・多面体 ・角錐、円錐 ・面の平行移動・回転移動と立体 ・立体の展開図 ・立体の表面積と体積 ⑮角柱と円柱 ・角柱、円柱の定義 ・角柱、円柱の底面、側面の関係 の考察 ・角柱、円柱の展開図、見取図




円柱の体積と表面積の求め方 展開図とイラストで分かりやすく解説




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット
1年 円柱の表面積|数学イメージ動画集|大日本図書 円柱の表面積を求めてみます。 円柱を展開してみると,円が2つと長方形になることがわかります。 したがって,この円柱の表面積は,底面である2つの円の面積と側面積を合わせたものになります。 実施時期 1年生3学期(2月) 単元項目 6章3節 立体の表面積と体積17/2/15 算数図形編 でる度⇒ ★〈円柱・円すい・展開図・切断〉円すいが切り取られた形は相似を使おう 下の図のような円すい台(円すいを底面と平行な面で切ったとき底面を含む立体)の体積は何cm 3 ですか。10 右の図のおうぎ形を,AO を軸として回転させてできる立体の 体積と表面積を求めなさい。 3cm 3cm A B O 円錐の展開図をかくと,右の図のようになる。 おうぎ形の中心角をa°とすると, 2π×2=2π×6× a 360 a=1 π×62× 1 360 =12π(cm2)




角柱 円柱の表面積と体積の公式 数学fun




三角柱と円柱の展開図をかこう 家庭学習レシピ
N n n 3歩歩けば忘れます。 H T Kr = (ީ i >{ͱ?19/2/21 2 次の展開図を組み立てて、できあがる立体の体積を求めましょう。 ① 式 長方形の横の長さは、円周と同じ長さなの積分で円柱をナナメに切るヤツの式の立て方が分からないです。 (0,1,0) $ を含む方の体積を求めよ。 大事なのは 点q の座標の求め方です。 実際に図を描いてみることで 点q がどうなるのかを確認して座標を求めましょう。 →角柱の体積展開図を描くと,右図のように側面は縦の長さが 8 cm,横の長さが(底面の円周の長さ) 2π×5 cmの長方形になるから,その面積は 8×2π×5=80π (cm 2) (答) →閉じる← 要点12 ≪円錐の側面積≫ 円錐の側面積を求めるには,まず展開図の扇形を描いて,その中心角を求めることから始めるとよい. 右図のように底面の半径が r ,母線の長さが L である円錐の



Kistenkasten723 123takashi 図形の包摂関係も 当時は ヴェン図で教えられていました T Co Evzapyw8h0 掛算 超算数 算数 算数教育 図形 包摂関係 長方形 回転 立体 Twitter




3分で分かる 円柱の体積 表面積の公式についてわかりやすく 合格サプリ
角柱や円柱を立体から展開して、どのような展開図になるかアニメーションで視覚的に 学習する 教材です。 (Windows・iOS 対応版)すい体の体積 すい体の体積 = 底面積 × 高さ ÷ 3 すい体の体積ですが、体積の単元自体は小学5年生の算数から始まり、6年生では円柱や角柱の体積を学習しています。 そして中学1年生になると、円柱や角柱から少し発展した、この「すい体」という立体に球の体積が外接する円柱叩積の言になるという定理をアルキメデスは力学的 に次のように証明する。図4でpqを軸として円0βqβ′と正方形且アサ′且′を 回転すると球 と倍の半径の円柱ができ、三角形0ガガ′を回転して円錐ができる。




簡単 円柱の体積公式は底面積 高さ 必ず解きたい計算問題付き 高校生向け受験応援メディア 受験のミカタ




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット
立体の見方 立体を普通に見えるように描いた図を 見取り図(みとりず) と言い、立体の面をダンボールの箱を崩すように開いて平面にしたものを 展開図(てんかいず) と言います。四角錐の展開図を書いてみましょう。底面が四角形で、側面が三角形ですから、中心が四角形で、四角形の右の図のように、底面が円である場合には、円柱といいます。 底面 側面 底面 例題1 -2 次の立体の展開図をかきなさい。 (1) 三角柱 (2) 円柱 <解説> 展開図をかくには、見取り図から、面全体がばらばらにならないように、辺にそって切り離していく空間図形 投影図 166 1 次のア~イに入る言葉を右下の答えのらんに書きましょう。 2 次の図のように円柱を置くとき、立面図と平面図はそれぞれ どんな図形になりますか。言葉や名称で答えなさい。 立体を平面上に表す方法として、見取り図や展開図の他に、立体をある方向から
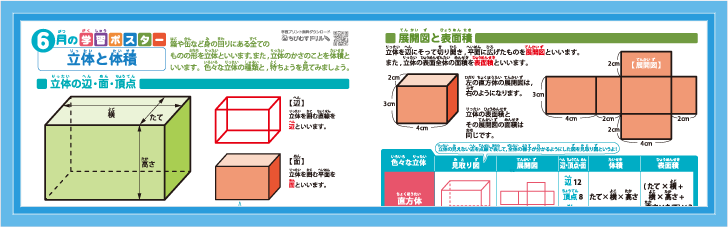



小学算数 立体と体積 直方体 立方体 三角柱 円柱 四角すい 円すい 辺 面 頂点 展開図 体積と表面積の公式 学習ポスター クイズテスト やってみよう ちびむすドリル 小学生学習ポスター テスト 家庭学習シート 3ステップ学習




計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
直方体の横の長さと体積の関係 いろいろな体積の単位 いろいろな単位・およその単位 力をつけよう(1) 力をつけよう(2) 3 小数のかけ算 小数をかけることの意味 問題一括 (5,408Kb) 解答一括 (5,539Kb) 小数×小数 筆算のしかた かける数と積の大きさ 面積 円柱の体積の公式 V=πr 2 hって? 円柱の体積の求め方を確認したところで、円柱の体積の公式についてふれておきましょう。 ある円柱において、底面の円の半径を r 、高さを h 、その円柱の体積を V とすると、V=πr 2 h この公式は、これまでに説明してきた求め方にしたがうことで簡単に導くことができます。 (底面の円の面積)=(半径)×(半径)×円柱の展開図の書き方を教えます。 問題 動画を見せながら、円柱の 展開図のかき方を教えます 動画作成協力・・動くイラストフリー素材 かき方がわかったら、上の円柱の 展開図を自分でかかせます。 ↑のような図が書ければ合格です。 書き方のコツ



展開図から求める体積 算数解法の極意




動画で学習 2 角柱と円柱の展開図 算数
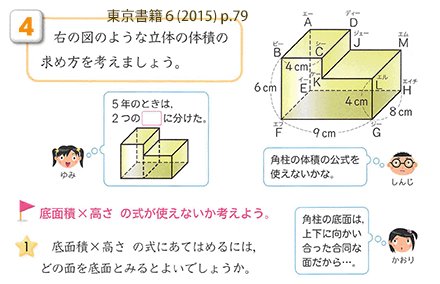
・展開図の素地 方と公式 ・体積の概測 ・高さと体積の関係 ・角柱、円柱の定義 ・角柱、円柱の底面、側面の関 係の考察 ・角柱、円柱の展開図、見取図 はこの形 点 直方体と立方体 ・直方体、立方体の概念と性質 ・直方体、立方体の展開図小学6年生の算数角柱や円柱の体積の求め方・公式の練習問題プリントを無料ダウンロード・印刷 (プリント5枚) 小学6年生の算数 図形の拡大と縮小拡大図と縮図 問題プリント体積・表面積⑵ 角柱 1 ステップ1 角柱の体積 1 図1のように、地面に置かれた図形があります。この図形を、図2のよ うに真上に移動させます。このとき図形が動いてできたあとは、図3のよ うな立体になります。この立体を、「柱 ちゅう




動画で学習 2 角柱と円柱の展開図 算数




角柱 円柱の表面積の求め方 中学数学の柱体の公式と展開図の計算 リョースケ大学
4 図は円柱の展開図です。このとき、次の問いに答えなさい。 (1)この円柱の側面積は何cm2ですか。 (2)この円柱の体積は何cm3ですか。 (答)(1)3768cm2 (2)cm3 ※ 立方体は3組の平行な正方形で囲まれた図形です。




Sqrt3 5 Descubre Como Resolverlo En Qanda
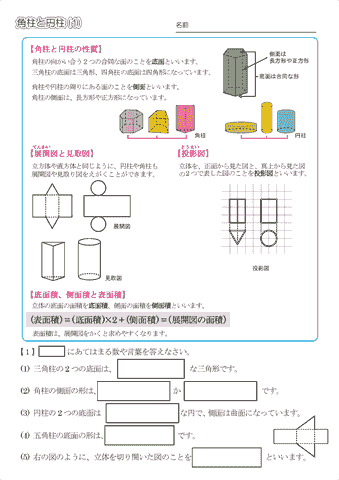



小学5年生の算数 角柱と円柱 問題プリント ちびむすドリル 小学生



Studydoctor角柱や円柱の展開図の形 中学1年数学 Studydoctor
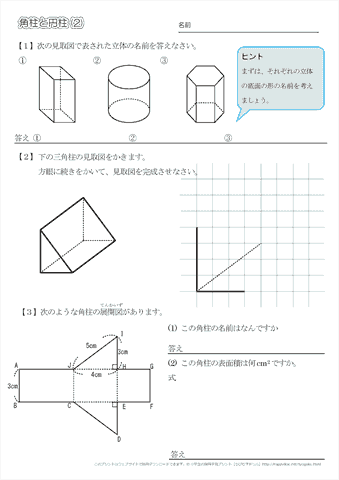



小学5年生の算数 角柱と円柱 問題プリント ちびむすドリル 小学生




円柱と円錐の性質と違い 中学数学 By じょばんに マナペディア




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
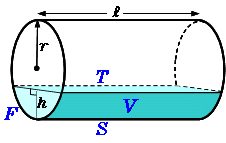



一部が欠けた直円柱の体積 高精度計算サイト




円柱の展開図 Youtube




円柱の展開図 Youtube



1



Mathematics 空間図形 表面積 働きアリ




円柱の体積と表面積の求め方 展開図とイラストで分かりやすく解説




角柱 円柱の表面積と体積の公式 数学fun
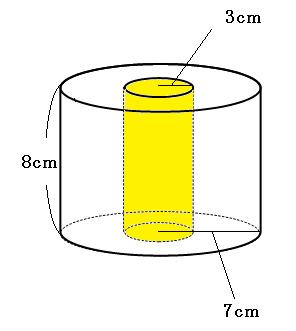



立体の表面積の求め方を解説 面倒な角柱や円柱の表面積をいかにサボって求めるか
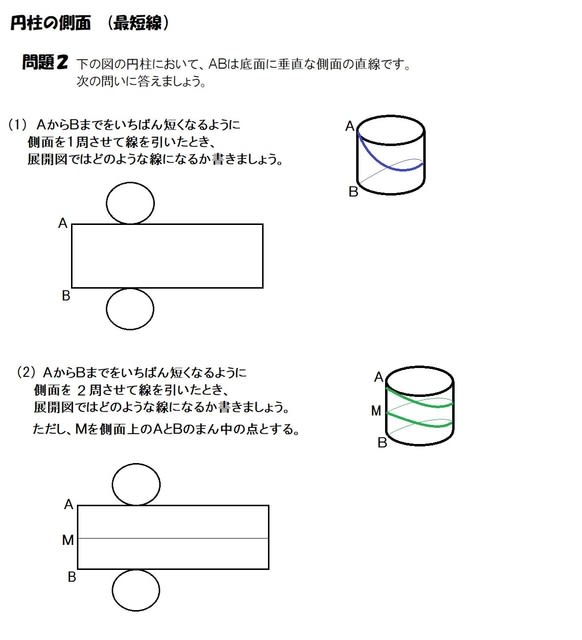



角柱と円柱 展開図を使う 小学5年 算数の教え方教えますmother S Math Happy Study Support
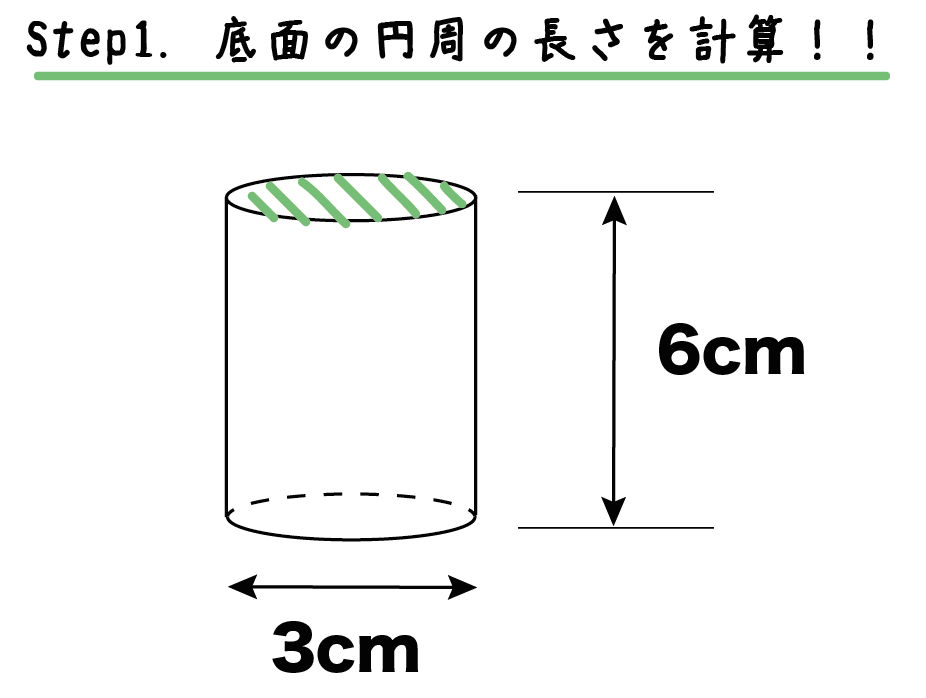



カンタン作図 円柱の展開図の書き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




算数 円柱の体積の求め方 公式で確認 小学生向け 数スタ



5 7 展開図から体積と表面積を求めるには さんすうがく パート 2



いろいろな立体の問題



円柱の展開図について 次の図は 円柱の展開図です ad Yahoo 知恵袋




小学算数 立体と体積 直方体 立方体 三角柱 円柱 四角すい 円すい 辺 面 頂点 展開図 体積と表面積の公式 学習ポスター クイズテスト やってみよう ちびむすマンスリー 学習ポスター テストクイズ 3ステップ学習 学習 算数 小学校 算数




5年算数角柱と円柱 2 いっちに算数 わかる教え方



下の図の円すいと円柱を合わせた立体の体積を求めなさい なお 円周率はpを用いる Yahoo 知恵袋



1



円柱を斜めに切った立体の展開図はどんな形か 算数解法の極意
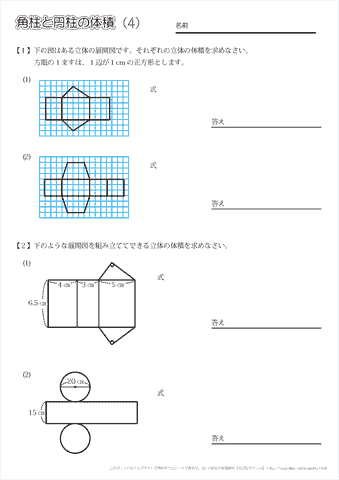



小学6年生の算数 角柱や円柱の体積の求め方 公式 問題プリント ちびむすドリル 小学生




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
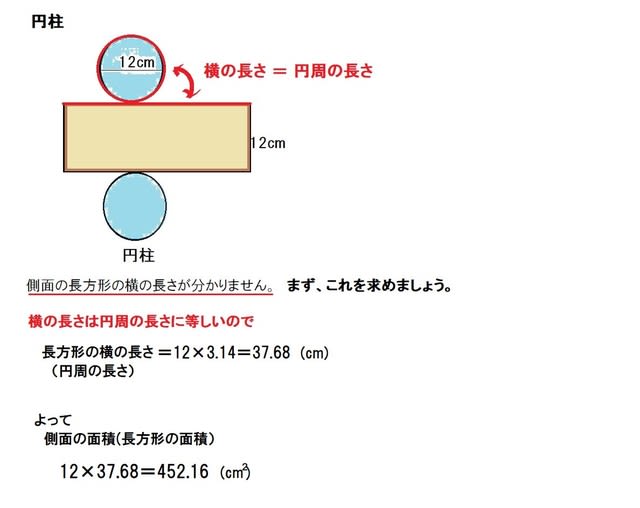



角柱と円柱 展開図を使う 小学5年 算数の教え方教えますmother S Math Happy Study Support




カンタン作図 円柱の展開図の書き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
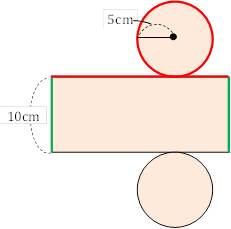



中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン



カンタン作図 円柱の展開図の書き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




なぜこの答えになるのか説明して欲しいです Clear
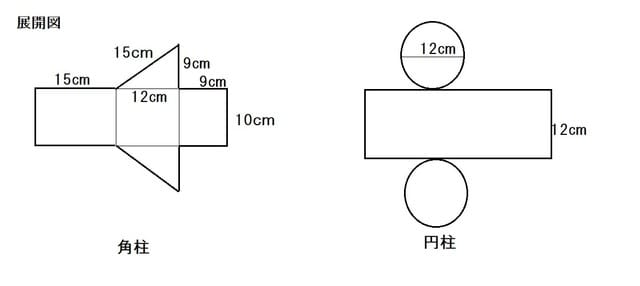



角柱と円柱 展開図を使う 小学5年 算数の教え方教えますmother S Math Happy Study Support



5年算数角柱と円柱 2 いっちに算数 わかる教え方




Descubre Como Resolverlo En Qanda
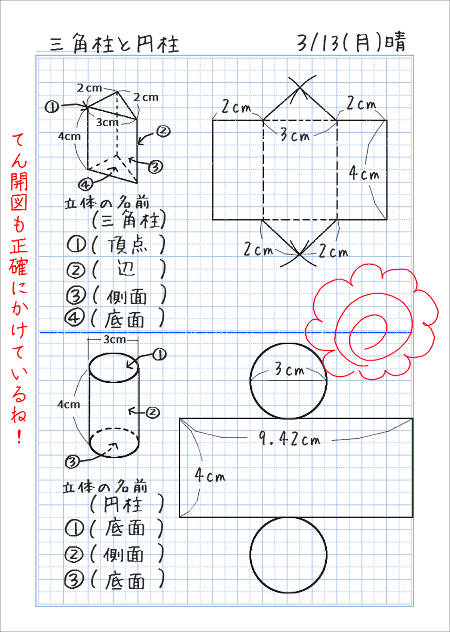



三角柱と円柱の展開図をかこう 家庭学習レシピ




円柱の体積と表面積の求め方 展開図とイラストで分かりやすく解説




立方体や直方体の体積の求め方を習ったら 少し応用的な問題にも取り組みましょう 展開図を見て 体積を求める問題や いくつかの立方体や直方体の面積を足したり引いたりして解く問題です 学習ノート 小学校 算数 学習
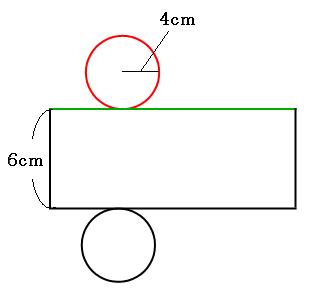



立体の表面積の求め方を解説 面倒な角柱や円柱の表面積をいかにサボって求めるか
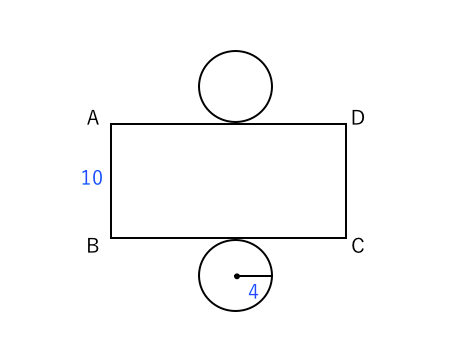



展開図を使った問題 苦手な数学を簡単に



柱体とすい体 中学受験 田中貴 Com




公式不要 円柱の側面積を3秒で計算できる求め方 Qikeru 学びを楽しくわかりやすく



Ss角柱と円柱の体積 Ss609 2 幼児 小学生教材のエジソンクラブ 通販 Yahoo ショッピング




求める立体の体積が円柱を二等分したものとありますが なぜそのようなことが言えるのでし Clear




空間図形 円柱の側面積の求め方がわかりません 中学数学 定期テスト対策サイト
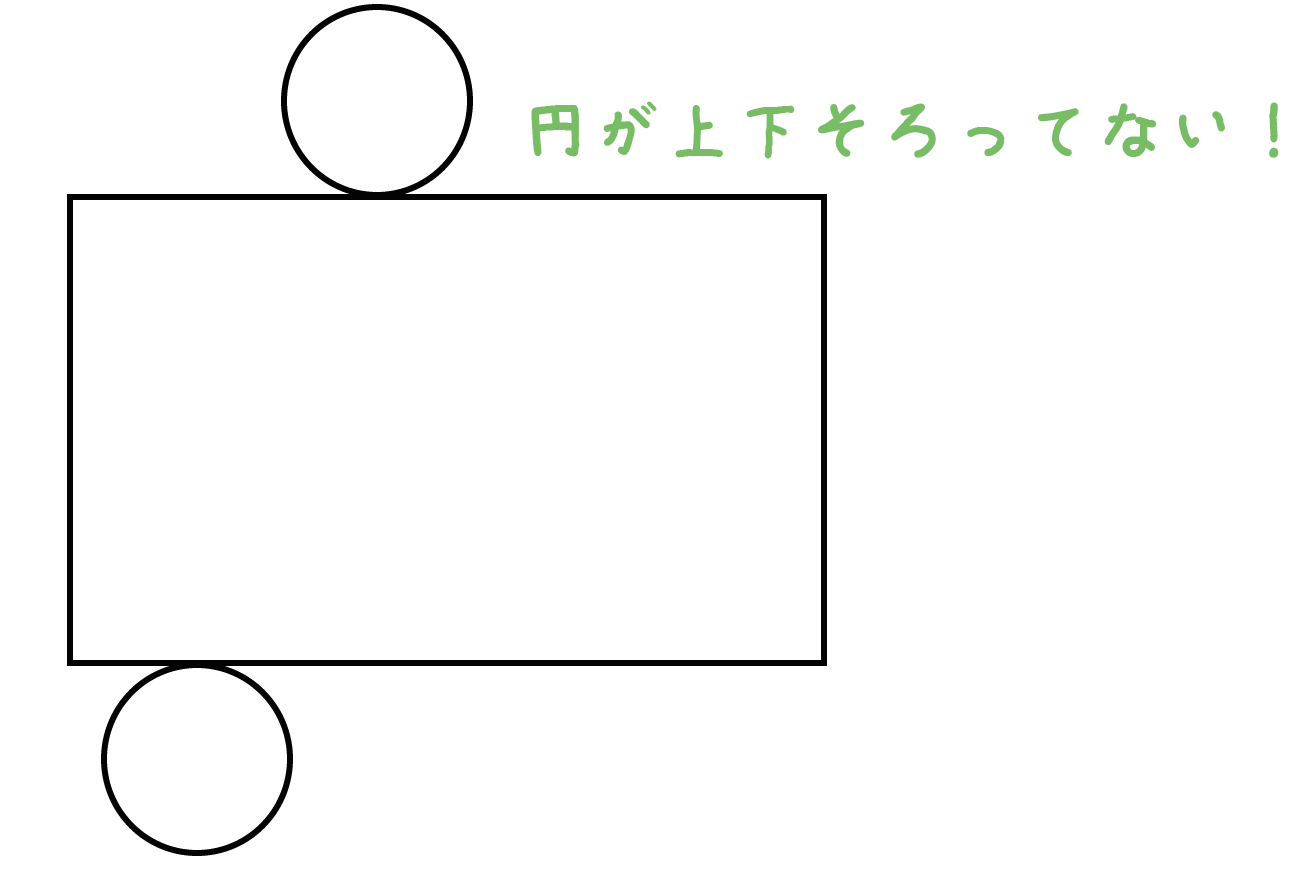



カンタン作図 円柱の展開図の書き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



円柱の斜め切断



花まるラボ スマホやタブレットで使える中学受験対策アプリ 究極の立体 展開 を発売 Edtechzine エドテックジン




角柱 円柱の表面積の求め方 中学数学の柱体の公式と展開図の計算 リョースケ大学
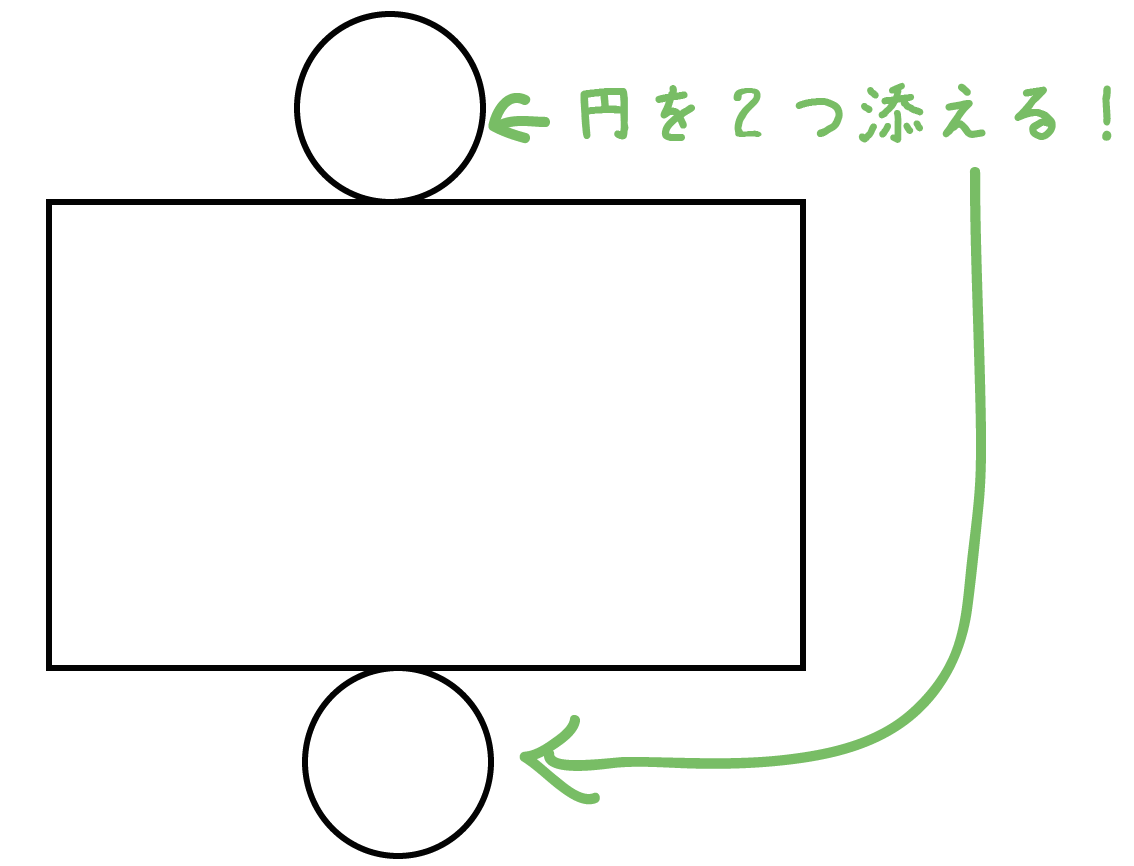



カンタン作図 円柱の展開図の書き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




高さの分からない円すい展開図 どうやって立体の体積を求めるの




円柱 円錐 球のcの求め方と公式 高校生向け受験応援メディア 受験のミカタ




円柱の表面積の求め方 公式と計算例
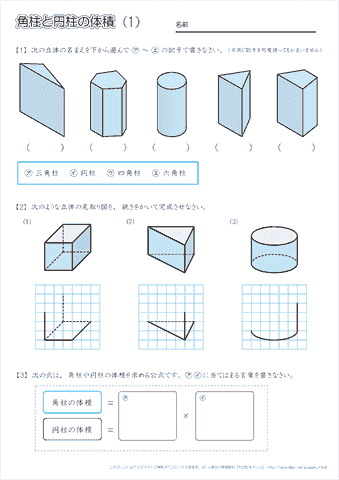



小学6年生の算数 角柱や円柱の体積の求め方 公式 問題プリント ちびむすドリル 小学生
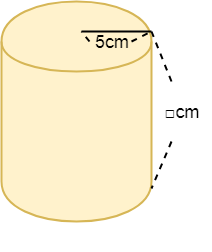



円柱の体積の求め方 公式 小学生 中学生の勉強



この展開図を組み立てた円柱の体積を教えてください 円柱の体積 Yahoo 知恵袋




中1数学 三角柱 四角柱の表面積の求め方がサクッとわかる 映像授業のtry It トライイット
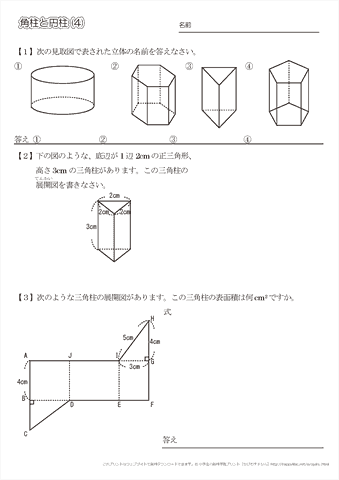



小学5年生の算数 角柱と円柱 問題プリント ちびむすドリル 小学生




中1数学 立体の表面積と体積の求め方と練習問題 Pikuu
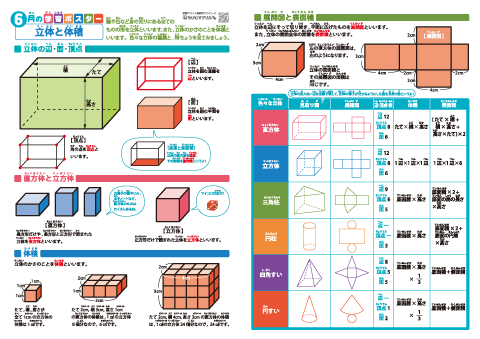



小学算数 立体と体積 直方体 立方体 三角柱 円柱 四角すい 円すい 辺 面 頂点 展開図 体積と表面積の公式 学習ポスター クイズテスト やってみよう ちびむすドリル 小学生学習ポスター テスト 家庭学習シート 3ステップ学習




円柱の表面積の求め方は ちょっと面倒くさいだけ たぬぬ塾 中学校の先生たち
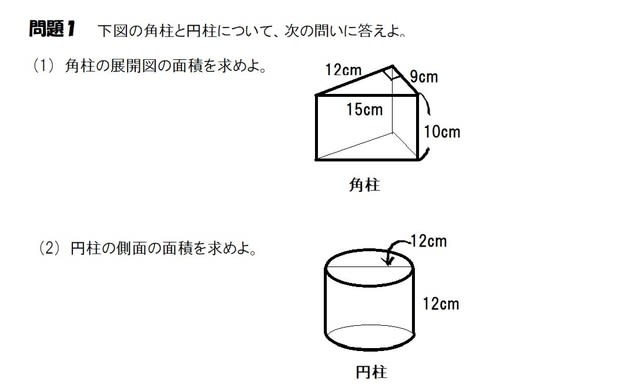



角柱と円柱 展開図を使う 小学5年 算数の教え方教えますmother S Math Happy Study Support
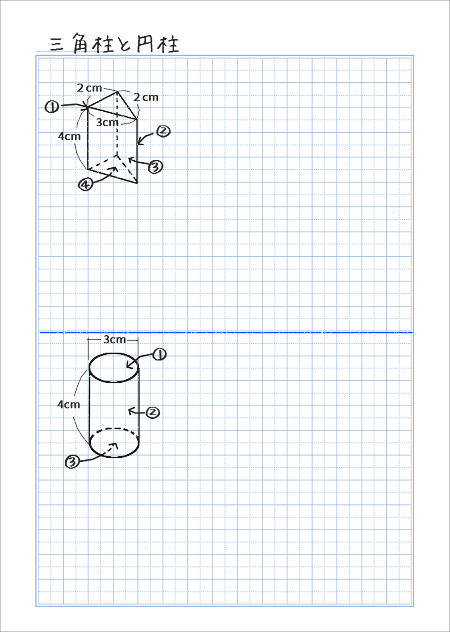



三角柱と円柱の展開図をかこう 家庭学習レシピ




円柱の展開図 Youtube
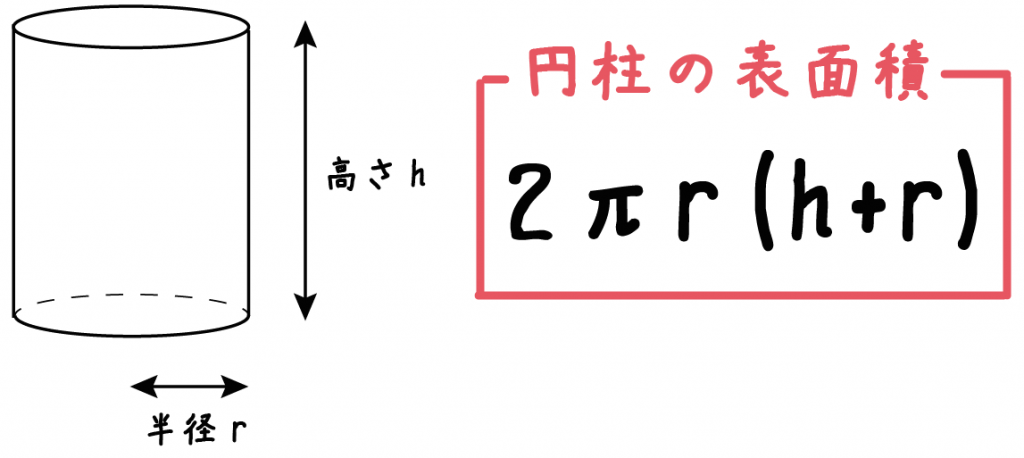



簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
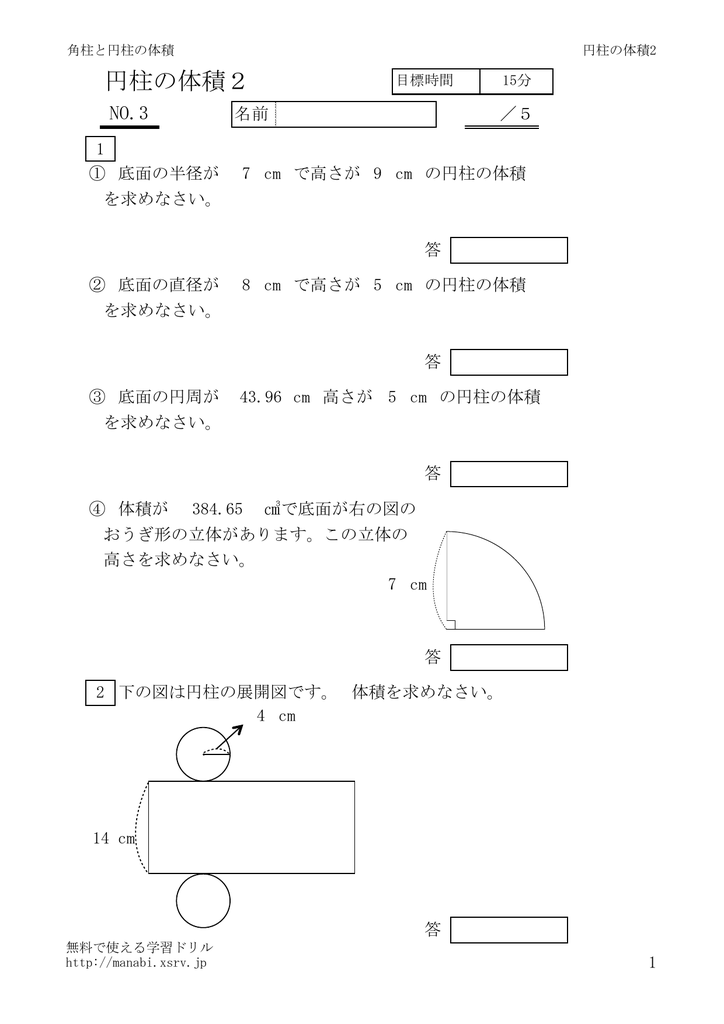



円柱の体積2 無料で使える学習ドリル




角柱 円柱の表面積の求め方 中学数学の柱体の公式と展開図の計算 リョースケ大学



3




立体の表面積 無料で使える中学学習プリント




角柱 円柱の体積の公式 小学生に教えるための分かりやすい解説 数学fun



中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン
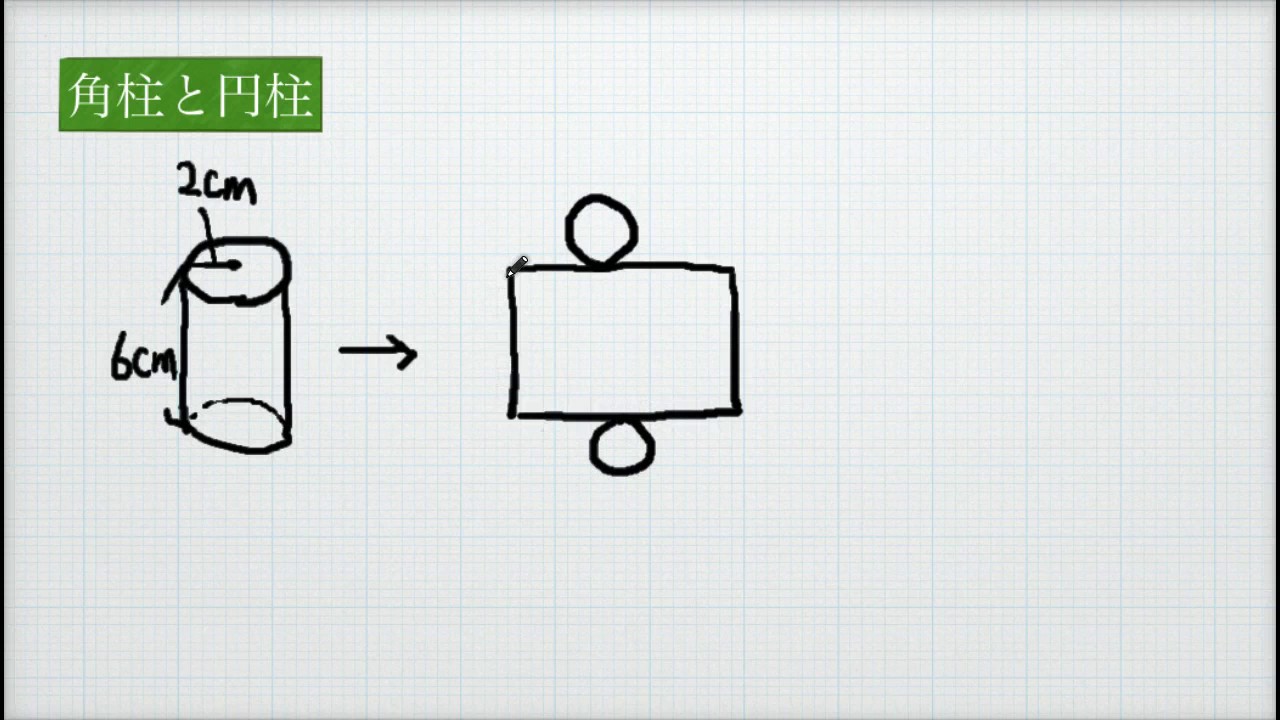



小学校5年 算数 円柱の展開図 Youtube



1



学習支援 まなびの函 中1 空間図形 3 立体の表面積
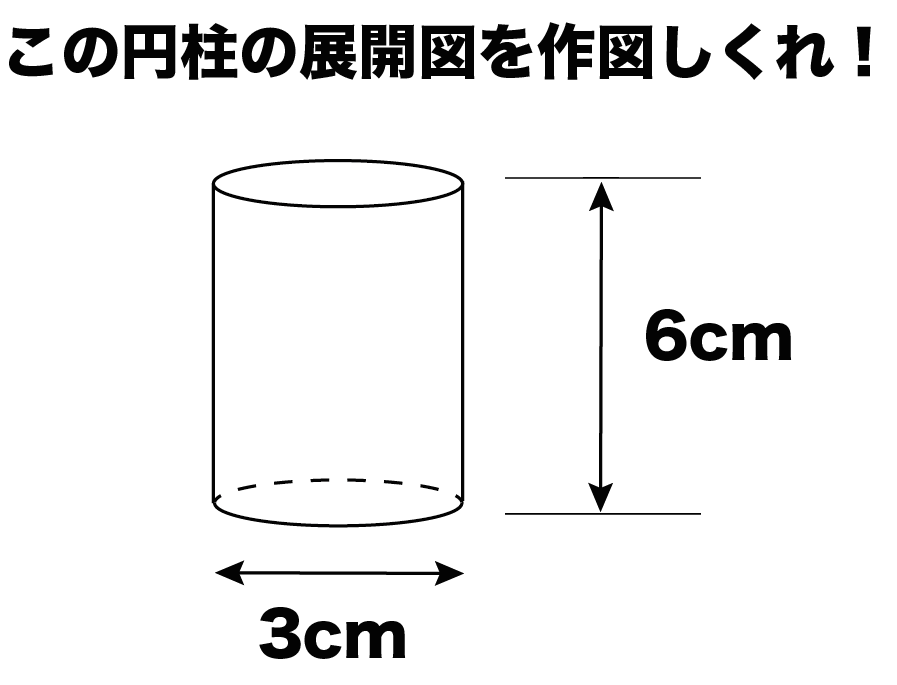



カンタン作図 円柱の展開図の書き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




円柱 円錐 球のcの求め方と公式 高校生向け受験応援メディア 受験のミカタ




円柱の表面積と体積を求める公式 具体例で学ぶ数学




角柱 円柱の表面積の求め方 中学数学の柱体の公式と展開図の計算 リョースケ大学




円柱の展開図 Youtube




円柱の表面積の求め方は ちょっと面倒くさいだけ たぬぬ塾 中学校の先生たち




算数図形編 円柱 円すい 展開図 切断 立体図形を切断したときの切り口を考えよう 中学受験 高校受験パスナビ




円柱の表面積と体積を求める公式 具体例で学ぶ数学




円柱の表面積の求め方 公式と計算例




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
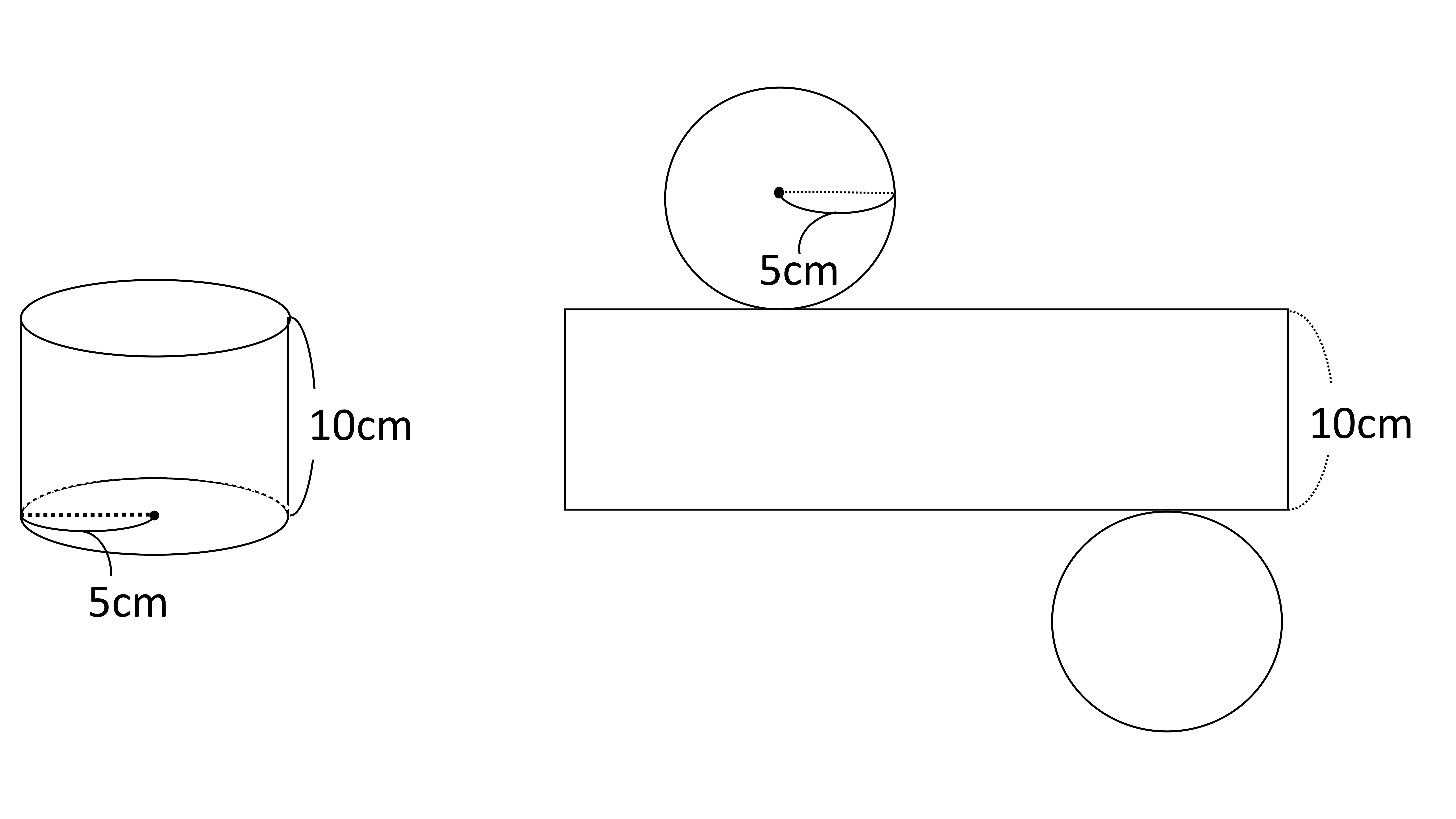



1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン




簡単 円柱の体積公式は底面積 高さ 必ず解きたい計算問題付き 高校生向け受験応援メディア 受験のミカタ



5年算数角柱と円柱 2 いっちに算数 わかる教え方




簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン



0 件のコメント:
コメントを投稿